déterminer tous les couples
Determiner tous les couples
4 messages
- Page 1 sur 1
determiner tous les couples
par mathlegend » 26 Nov 2010, 15:39
bonjour
déterminer tous les couples)
d'entiers naturels non-nuls tels que
^2}{(x+y)^2})
soit un entier naturel
déterminer tous les couples
par Ben314 » 26 Nov 2010, 17:51
Salut,
Poson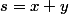t
et 
(étonant, non...)
^2}{(x+y)^2}<br />=\dfrac{s^3-3sp-p^2}{s^2}<br />=s-\dfrac{4p^2+12sp+9s^2-9s^2}{4s^2}<br />=s-\dfrac{1}{4}\left(\left(\dfrac{2p+3s}{s}\right)^2-9\right))
est entier ssi 
est un entier dont le carré est congru à 9(=1) modulo 4 (car, si 
est tel que 
alors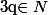 
).
Il faut (et il suffit) donc que
soit un entier impair, c'est à dire que 
soit entier : 
où 
.
Si on pose
, 
alors 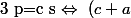(c+b)=c\left((c+a)+(c+b)\right)\ \Leftrightarrow\ ab=c^2)
.
Les solutions sont donc les couples)
tels que 
, 
avec 
Posont
Il faut (et il suffit) donc que
Si on pose
Les solutions sont donc les couples
Modifié en dernier par Ben314 le 04 Juil 2023, 19:28, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 26 Nov 2010, 20:18
Tient, je vient de me rendre compte que j'ai oublié un "détail" : la fraction doit être un entier naturel, c'est à dire positif.
Il y a sans doute nettement plus simple dans ce cas, mais on peut aussi continuer "dans la foulée" :
^2}{(x+y)^2}<br />=s-\frac{3sp+p^2}{s^2}<br />=(a+c)+(b+c)-3c-c^2s<br />=a+b-ab-c)
On doit donc avoir
donc (b-1)\leq 0)
, c'est à dire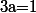 
(ou 
).
D'où
et 
doit être positif donc on doit prendre 
et la seule solution est 
qui donne ^2}{(x+y)^2}=0)
Il y a sans doute nettement plus simple dans ce cas, mais on peut aussi continuer "dans la foulée" :
On doit donc avoir
D'où
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :