vam edit > ** titre modifié**
Démontrer cette inégalité
6 messages
- Page 1 sur 1
Re: Démontrer cette inégalité
C'est FAUX : pour 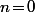 le terme de gauche est
le terme de gauche est +\frac{1}{2}\ln(1\!+\!x^2)) qui tend vers
qui tend vers  lorsque
lorsque 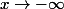 alors que le terme de droite tend vers 0.
alors que le terme de droite tend vers 0.
Modifié en dernier par Ben314 le 31 Mar 2024, 13:24, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Démontrer cette inégalité
Il y a aussi le fait que dans la somme du terme de gauche le terme général est !})
autrement dit l'exposant de t est un impair, comment donc obtenir t² par exemple ?
autrement dit l'exposant de t est un impair, comment donc obtenir t² par exemple ?
Re: Démontrer cette inégalité
La façon dont je vois l'énoncé, c'est ça :
\dfrac{1}{1+t^2}\,dt\leqslant{\dfrac{\big(\exp(x)-1\big)\arctan{x}}{x})
où on somme sur tout les entiers jusqu'à un certain entier impair
jusqu'à un certain entier impair 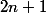 .
.
Pour le il est fort probable que ce soit
il est fort probable que ce soit  , mais pour le
, mais pour le  c'est plus que louche : si on se restreint à
c'est plus que louche : si on se restreint à 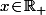 alors la somme dans l'intégrale est croissante en
alors la somme dans l'intégrale est croissante en  donc l'inégalité est vraie pour tout n si et seulement si elle est vrai pour la limite
donc l'inégalité est vraie pour tout n si et seulement si elle est vrai pour la limite 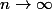 , c'est à dire pour
, c'est à dire pour ) à la place de la somme. La somme ne sert donc à rien et le
à la place de la somme. La somme ne sert donc à rien et le  encore moins.
encore moins.
SI on accepte les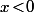 , alors la somme alterne les +,-, il n'est pas clair qu'elle soit croissante (en
, alors la somme alterne les +,-, il n'est pas clair qu'elle soit croissante (en  ) et le fait qu'on s’arrête à
) et le fait qu'on s’arrête à  prend du sens. Sauf que le résultat est faux dans ce cas . . .
prend du sens. Sauf que le résultat est faux dans ce cas . . .
où on somme sur tout les entiers
Pour le
SI on accepte les
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Démontrer cette inégalité
Je me demande si cela ne serait pas :
!}\Big)\dfrac{1}{1+t^2}\,dt\leqslant{\dfrac{\big(\exp(x)-1\big)\arctan{x}}{x})
L'avantage c'est que cela fait disparaitre t/1! qui posait un problème en donnant ln(1+x²).
De plus on peut trouver une relation de récurrence entre la primitive de!} \times \dfrac{1}{t^2+1}) et celle de
et celle de }}{(2(k-1))!} \times \dfrac{1}{t^2+1})
L'avantage c'est que cela fait disparaitre t/1! qui posait un problème en donnant ln(1+x²).
De plus on peut trouver une relation de récurrence entre la primitive de
Re: Démontrer cette inégalité
Soit 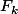 une primitive sur R de
une primitive sur R de telle que
telle que =\dfrac{t^{2k}}{(2k)!} \times \dfrac{1}{t^2+1})
et soit=\sum_{k=0}^{n}{F_k(x)})
Les sont les fonctions apparaissant dans le membre de droite de l'inégalité
sont les fonctions apparaissant dans le membre de droite de l'inégalité
On a
! f_k(t)=t^{2k-2}-\dfrac{t^{2k-2}}{t^2+1})
donc
! F_k(t)=\dfrac{t^{2k-1}}{2k-1}-(2k-2)!F_{k-1}(t))
De plus=arctan(x)=S_0(x))
donc pour k=1:
=t-F_0(t)=t - arctan(t))
et=F_0(x)+F_1(x)=arctan(x)+\frac{x}{2}-\frac{1}{2}arctan(x)=\frac{x}{2}+\frac{1}{2}arctan(x))
pour k=2
=\dfrac{t^{3}}{3}-2!F_1(t)=\dfrac{t^{3}}{3}-(t - arctan(t)))
et=F_0(x)+F_1(x)+F_2(x)=\frac{x}{2}+\frac{1}{2}arctan(x)+\frac{x^{3}}{72}-\frac{1}{24}(x - arctan(x))<br />=\frac{11x}{24}+\frac{x^{3}}{72}+\frac{13}{24}arctan(x))
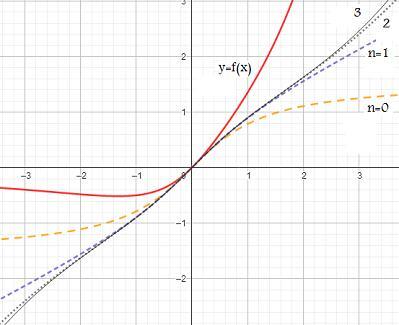
Sur la figure ci-dessous j'ai représenté la fonction f du membre de droite en rouge, et les fonctions pour n= 0,1,2,3
pour n= 0,1,2,3
On peut remarquer qu'elles sont au dessous mais plutôt proches au voisinage de 0.
Reste à le démontrer...
et soit
Les
On a
donc
De plus
donc pour k=1:
et
pour k=2
et
Sur la figure ci-dessous j'ai représenté la fonction f du membre de droite en rouge, et les fonctions
On peut remarquer qu'elles sont au dessous mais plutôt proches au voisinage de 0.
Reste à le démontrer...

6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
