Le demi-sucre de Zac Haroz.
26 messages
- Page 1 sur 2 - 1, 2
Le demi-sucre de Zac Haroz.
Zac Haroz vient d'acheter un paquet de sucre en morceaux. Tout les matin il met un demi-sucre dans son café. Pour ce faire, il pioche au hasard (*) un morceau de sucre dans le paquet et, si c'est un morceau entier, il le coupe en deux et remet un des demi-sucre dans la boite. Bien sûr, le premier matin il prend forcément un sucre entier et, tout aussi clairement, le dernier matin, il prend un demi sucre vu qu'il ne reste forcément que ça dans boite !!!
Mais quelle est la probabilité qu'il pioche un demi-sucre dans la boite l'avant-dernier matin ?
(*) Deux interprétations possibles à étudier toutes les deux :
1- Soit tout les morceaux de sucres (entier ou demi) ont la même proba. d'être tirés.
2- Soit la proba. est proportionnelle au volume du morceau (donc double pour les sucres entiers)
On pourra éventuellement chercher uniquement la probabilité asymptotique lorsque le nombre de sucre (de départ) tend vers l'infini
P.S. : J'ai une solution très simple pour une des deux interprétations, mais pas pour l'autre...
Mais quelle est la probabilité qu'il pioche un demi-sucre dans la boite l'avant-dernier matin ?
(*) Deux interprétations possibles à étudier toutes les deux :
1- Soit tout les morceaux de sucres (entier ou demi) ont la même proba. d'être tirés.
2- Soit la proba. est proportionnelle au volume du morceau (donc double pour les sucres entiers)
On pourra éventuellement chercher uniquement la probabilité asymptotique lorsque le nombre de sucre (de départ) tend vers l'infini
P.S. : J'ai une solution très simple pour une des deux interprétations, mais pas pour l'autre...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Le demi-sucre de Zac Haroz.
L'interprétation 2 est effectivement très facile à traiter, et ça a l'air plus coton pour la 1.
Re: Le demi-sucre de Zac Haroz.
j'ai (1 - (1+t)\exp(-t))^{n-1} dt) de piocher un sucre entier l'avant dernier jour pour la première interprétation mais je sais pas trop quoi faire avec ensuite. Peut-être regarder si en développant puis en intégrant y'a des simplifications magiques.
de piocher un sucre entier l'avant dernier jour pour la première interprétation mais je sais pas trop quoi faire avec ensuite. Peut-être regarder si en développant puis en intégrant y'a des simplifications magiques.
Re: Le demi-sucre de Zac Haroz.
Je n'ai pas réfléchi au probléme mais en faisant confiance au résultat de Doraki j'obtiens pour l'assymptotique l'équivalent 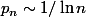
Re: Le demi-sucre de Zac Haroz.
Je n'ai pas compris la réponse de Doraki, mais je crois bien que la proba de piocher un 1/2 sucre augmente avec n, de manière assez significative au début.
Re: Le demi-sucre de Zac Haroz.
Bonjour tous,
On peut aussi s'intéresser à l'évolution de la probabilité de tirer 1/2 sucre au fur à mesure que l'on vide la boite, je viens de terminer la mienne :

on termine pas loin de 0,87
Et avec une plus grosse boite ?

Les courbes se ressemblent, mais ce coup ci on termine vers les 0,93
J'ai tracé aussi le moment où on atteint la proba de 0,5 : c'est autour de de 0,89 *nb_de _sucres dans les deux cas ...
Si tout ça vous inspire !
On peut aussi s'intéresser à l'évolution de la probabilité de tirer 1/2 sucre au fur à mesure que l'on vide la boite, je viens de terminer la mienne :
on termine pas loin de 0,87
Et avec une plus grosse boite ?
Les courbes se ressemblent, mais ce coup ci on termine vers les 0,93
J'ai tracé aussi le moment où on atteint la proba de 0,5 : c'est autour de de 0,89 *nb_de _sucres dans les deux cas ...
Si tout ça vous inspire !
Re: Le demi-sucre de Zac Haroz.
J'ai bien un résultat similaire à 0,88.... pour 310 sucres.
Étonnant final pour la courbe à 50 000 sucres.....
Étonnant final pour la courbe à 50 000 sucres.....
Re: Le demi-sucre de Zac Haroz.
Après livraison de mon camion de sucre,
Je confirme le final :

La proba de 0,5 est atteinte pour x/n =0,896386718750000 ce qui semble la limite, et n’évolue plus dans mes tirages, ( ce qui correspond à 7343/8192...)
J'ai tracé en orange la partie qui évolue de façon 'fortement linéaire'
Et pour la limite asymptotique que demande Ben314 :

ou en changeant d'échelle:

Difficile à voir si on va dépasser le 0,95 et se rapprocher de 1..
Il faudrait que j'achète quelques camions de plus ... pas facile à stocker....
Je confirme le final :
La proba de 0,5 est atteinte pour x/n =0,896386718750000 ce qui semble la limite, et n’évolue plus dans mes tirages, ( ce qui correspond à 7343/8192...)
J'ai tracé en orange la partie qui évolue de façon 'fortement linéaire'
Et pour la limite asymptotique que demande Ben314 :
ou en changeant d'échelle:
Difficile à voir si on va dépasser le 0,95 et se rapprocher de 1..
Il faudrait que j'achète quelques camions de plus ... pas facile à stocker....
Re: Le demi-sucre de Zac Haroz.
Quand je disais étonnant pour la fin de courbe, ce n'était pas un doute sur la véracité du calcul.
Donc le 1 comme limite n'est pas du tout sûr......
Donc le 1 comme limite n'est pas du tout sûr......
Re: Le demi-sucre de Zac Haroz.
Programme d'un autre intervenant ( je ne garantis pas son exactitude ) et quelques résultats:
u=0
u1=u
v1=100000000
v=v1
for i in range(1,2*v1):
u1=u
u=(u*(u-1)+v*(u+1))/(v+u)
v=(u1*v+v*(v-1))/(u1+v)
print((1-v/u)*100)
10.000 : 92.08%
100.000 : 93.36%
1.000.000 : 94.27%
10.000.000 : 94.97%
u=0
u1=u
v1=100000000
v=v1
for i in range(1,2*v1):
u1=u
u=(u*(u-1)+v*(u+1))/(v+u)
v=(u1*v+v*(v-1))/(u1+v)
print((1-v/u)*100)
10.000 : 92.08%
100.000 : 93.36%
1.000.000 : 94.27%
10.000.000 : 94.97%
Re: Le demi-sucre de Zac Haroz.
Ton programme essaye de calculer pour chaque jour l'espérance du nombre de demi-sucres u et du nombre de sucres v mais ça n'est pas possible sans avoir des informations plus précises sur la distribution du nombre de sucres (ou de demi-sucres), parceque la moyenne de a/b ce n'est pas la même chose que la moyenne de a / la moyenne de b.
C'est sûr que c'est dommage parceque ça permettrait d'avoir un algorithme de calcul de pn de complexité linéaire en n et pas quadratique.
ffpower c'est l'équivalent auquel je pensais aussi mais j'avais pas tellement le courage de regarder en détail.
Les graphes de l'espérance de la proportion de sucres entiers (ou de demi-sucres) au fil des jours sont intéressants, je vais y réfléchir
C'est sûr que c'est dommage parceque ça permettrait d'avoir un algorithme de calcul de pn de complexité linéaire en n et pas quadratique.
ffpower c'est l'équivalent auquel je pensais aussi mais j'avais pas tellement le courage de regarder en détail.
Les graphes de l'espérance de la proportion de sucres entiers (ou de demi-sucres) au fil des jours sont intéressants, je vais y réfléchir
Re: Le demi-sucre de Zac Haroz.
nodgim a écrit:Programme d'un autre intervenant ( je ne garantis pas son exactitude ) et quelques résultats:
J'ai été déstabilisé parce que , le programme présenté était trivial, et les résultats me semblaient corrects ...
Mais Doraki m'a remonté le moral , et mon programme est bien en complexité n² ...
J'ai quand même regardé si ce programme pouvait être un bon approximant :
Nodgim : le programme que tu montres ne semble pas celui qui a généré les résultats ... je ne retrouve pas les résultats avancés, de plus la proba finale devrait ressembler à v/(v+u), et non pas (1-v/u), et qui plus est sauf erreur on ne termine pas sur une espérance de 1 au dernier tirage ( ce que doit dire Doraki)..
Tu confirmes?
Re: Le demi-sucre de Zac Haroz.
Je partage ton doute. C'est parce qu'il donnait des résultats assez proches de tes graphes que je l'ai communiqué. C'est en effet un algorithme linéaire qui passe de moyenne en moyenne, alors que le calcul réel est à 2 dimensions ( se prête bien à un tableur).
Re: Le demi-sucre de Zac Haroz.
Bonjour,
J'ai quand même regardé, ce que donnait "l'approximation" (calculée en complexité linéaire)...
En fait c'est pas mal du tout, car ca donne visiblement un majorant, assez facile à calculer à notre série

Alors, si on veut 'au moins ' vérifier que l'on va dépasser le 0,95, certainement qu'il faut partir sur 10^8 sucres... et là çà coince dans les ordis....
@Nogim,
- on attend les résultats de Scarta pour confirmer, mais le million ne va pas être suffisant pour conclure...
- personne ne semble s'être attaqué au problème du nombre de tirage qui nous amène à une proba de 1/2 ? ( ma conjecture de x/n = 7343/8192)...
@ben314
- j'espère que tu vas bien, et que attends tranquillement en savourant ton café..
- si jamais un demi sucre n'est pas raisonnable pour ta santé, je te propose de passer au quart de sucre:
si tu tires un sucre tu le casses en deux, et la moitié en deux encore et tu remets la moitié et le quart dans la boite,
si tu tires un demi sucre, tu le casses en deux et tu remets un quart dans la boite,
si tu tires un quart, c'est tout bon
et tu t'intéresses par exemple à la proba de trouver un demi sucre à l'avant denier tirage... ou un sucre entier 3 tirages avant la fin....
Ps - j'ai essayé de m 'intéresser à la "vague" de probabilité qui traverse les tirages, en gros une courbe "gausienne" pas très large , et en laissant tomber "les bords" dans mes calculs, pour essayer d'avoir un minorant à notre courbe, calculé en O(n) , sans y arriver....
J'ai quand même regardé, ce que donnait "l'approximation" (calculée en complexité linéaire)...
En fait c'est pas mal du tout, car ca donne visiblement un majorant, assez facile à calculer à notre série
Alors, si on veut 'au moins ' vérifier que l'on va dépasser le 0,95, certainement qu'il faut partir sur 10^8 sucres... et là çà coince dans les ordis....
@Nogim,
- on attend les résultats de Scarta pour confirmer, mais le million ne va pas être suffisant pour conclure...
- personne ne semble s'être attaqué au problème du nombre de tirage qui nous amène à une proba de 1/2 ? ( ma conjecture de x/n = 7343/8192)...
@ben314
- j'espère que tu vas bien, et que attends tranquillement en savourant ton café..
- si jamais un demi sucre n'est pas raisonnable pour ta santé, je te propose de passer au quart de sucre:
si tu tires un sucre tu le casses en deux, et la moitié en deux encore et tu remets la moitié et le quart dans la boite,
si tu tires un demi sucre, tu le casses en deux et tu remets un quart dans la boite,
si tu tires un quart, c'est tout bon
et tu t'intéresses par exemple à la proba de trouver un demi sucre à l'avant denier tirage... ou un sucre entier 3 tirages avant la fin....
Ps - j'ai essayé de m 'intéresser à la "vague" de probabilité qui traverse les tirages, en gros une courbe "gausienne" pas très large , et en laissant tomber "les bords" dans mes calculs, pour essayer d'avoir un minorant à notre courbe, calculé en O(n) , sans y arriver....
Re: Le demi-sucre de Zac Haroz.
Ravi de voir qu'on parle de moi 
Bref pour le million ça tourne encore, je pensais faire une version qui distribue un peu les calculs sur une étape (puisque l'étape précédente détermine entièrement l'étape courante, comme tout bon processus markovien) mais j'ai pas eu des masses le temps et vu la simplicité des calculs pour une seule étape je doute qu'on y gagne pour 1 million...
En gros, j'ai un tableau de taille 4N+2, la première moitié me sert à stocker l'état courant (2N+1 possibilités pour des demis sucres), et la seconde me sert à stocker l'état suivant. Je bascule de l'une à l'autre en alternant la "première" et la "seconde" moitié.
Ca me permet de faire une allocation unique et ne plus me soucier de la mémoire ensuite.
Et ma seconde boucle ne regarde que les valeurs "correctes" c'est à dire celles qui ont du sens : 60 demis sucres quand il n'en reste que 45 au plus est exclu par exemple.
Bref pour le million ça tourne encore, je pensais faire une version qui distribue un peu les calculs sur une étape (puisque l'étape précédente détermine entièrement l'étape courante, comme tout bon processus markovien) mais j'ai pas eu des masses le temps et vu la simplicité des calculs pour une seule étape je doute qu'on y gagne pour 1 million...
- Code: Tout sélectionner
double sucre(long sucres) {
long halves = sucres<<1;
halves ++;
double *prob = malloc(halves * sizeof(double) << 1);
for(int i=0; i< halves; i++) prob[i] = prob[halves + i] = 0;
int current = 0;
int previous = halves;
prob[0] = 1;
for(int total = halves - 2; total >= 2; total--) {
current = previous;
previous = halves - previous;
prob[current] = prob[previous+1] * 2 / (total + 2);
for(int i=1; i<= total; i++) prob[current+i] =
prob[previous+i+1] * 2 * (i+1) /(total + 2 + i) +
prob[previous+i-1] * (total - i + 2) / (total + i);
}
double res = prob[current+2];
free(prob);
return res;
}
En gros, j'ai un tableau de taille 4N+2, la première moitié me sert à stocker l'état courant (2N+1 possibilités pour des demis sucres), et la seconde me sert à stocker l'état suivant. Je bascule de l'une à l'autre en alternant la "première" et la "seconde" moitié.
Ca me permet de faire une allocation unique et ne plus me soucier de la mémoire ensuite.
Et ma seconde boucle ne regarde que les valeurs "correctes" c'est à dire celles qui ont du sens : 60 demis sucres quand il n'en reste que 45 au plus est exclu par exemple.
Re: Le demi-sucre de Zac Haroz.
Enfin ceci dit, Doraki a donné la formule au tout début (chapeau c'est bien vu !) donc ne vous attendez pas à un miracle la réponse sera 94,185%
Mon programme qui tourne encore a déjà sorti ça
10 : 0.761443
100 : 0.857820
1000 : 0.896716
10000 : 0.918266
100000 : 0.932128
Un autre bout de code avec la formule intégrale donne en quelques secondes
10^1: 0.761443
10^2: 0.857820
10^3: 0.896716
10^4: 0.918266
10^5: 0.932128
10^6: 0.941853
10^7: 0.949079
10^8: 0.954672
10^9: 0.959135
10^10: 0.962783
10^11: 0.965823
10^12: 0.968396
10^13: 0.970604
10^14: 0.972519
10^15: 0.974172
Après, pour la suite je dépasse la limite "long" faudrait que je réécrive une partie vite fait
Le code vite fait mal fait :
Mon programme qui tourne encore a déjà sorti ça
10 : 0.761443
100 : 0.857820
1000 : 0.896716
10000 : 0.918266
100000 : 0.932128
Un autre bout de code avec la formule intégrale donne en quelques secondes
10^1: 0.761443
10^2: 0.857820
10^3: 0.896716
10^4: 0.918266
10^5: 0.932128
10^6: 0.941853
10^7: 0.949079
10^8: 0.954672
10^9: 0.959135
10^10: 0.962783
10^11: 0.965823
10^12: 0.968396
10^13: 0.970604
10^14: 0.972519
10^15: 0.974172
Après, pour la suite je dépasse la limite "long" faudrait que je réécrive une partie vite fait
Le code vite fait mal fait :
- Code: Tout sélectionner
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
double sucre(long sucres);
double fastPow(double a, long b);
int main(int argc, char** argv) {
double i = 10;
for(int j = 1; j < 16; j++, i*=10)
printf("10^%d: %f\n", j, sucre(i));
}
double fastPow(double a, long b) {
double res = 1;
double c = a;
for(long i = b; i; i>>=1) {
if(i&1) res *= c;
c *= c;
}
return res;
}
double sucre(long sucres) {
double res = 0;
double limit = 10000;
double step = 0.001;
for(double i=0; i<limit; i += step) {
res += exp(-i) * fastPow(1 - (1+i)*exp(-i), sucres-1);
}
return 1 - res * sucres * step;
}
Re: Le demi-sucre de Zac Haroz.
scarta a écrit:En gros, j'ai un tableau de taille 4N+2, la première moitié me sert à stocker l'état courant (2N+1 possibilités pour des demis sucres), et la seconde me sert à stocker l'état suivant. Je bascule de l'une à l'autre en alternant la "première" et la "seconde" moitié..
Bonsoir Scarta,
Content de te causer, je te suis depuis longtemps 'sur un autre site'
oui il faut gérer aussi l'espace mémoire, je fais comme toi, mais avec 2 tableaux....
- Code: Tout sélectionner
next[col] += probaP * cur[col];
next[col + 1] += probaQ * cur[col];
en swapant mes deux tableaux
- Code: Tout sélectionner
//on swappe les lignes
{
double* tmp = cur;
cur = next;
next = tmp;
}
Mais ça c'est de la basse besogne..
scarta a écrit:Enfin ceci dit, Doraki a donné la formule au tout début (chapeau c'est bien vu !) donc ne vous attendez pas à un miracle la réponse sera 94,185%
Par contre là ... je suis scotché..
Doraki n'avait pas l'air à l'époque de savoir ce qu'il pouvait déduire de sa formule... ( où du moins il n'a pas pris la peine de le dire ..)
Tu m'expliquerais ?
Amitiés
Ps : une idée sur "ma conjecture " ?
Re: Le demi-sucre de Zac Haroz.
J'avoue que j'ai pas regardé encore ta conjecture...
L'intégrale susmentionnée donne la probabilité de tirer un sucre entier l'avant dernier jour tout simplement.
Calculée à l'arrache "en tranches" on trouve rapidement les résultats. Le plus compliqué est de gérer la puissance efficacement mais bon ça casse pas des briques non plus
Après le "comment on arrive à ce résultat", je rends à Cesar ce qui est à Cesar et laisse Doraki l'expliquer
L'intégrale susmentionnée donne la probabilité de tirer un sucre entier l'avant dernier jour tout simplement.
Calculée à l'arrache "en tranches" on trouve rapidement les résultats. Le plus compliqué est de gérer la puissance efficacement mais bon ça casse pas des briques non plus
Après le "comment on arrive à ce résultat", je rends à Cesar ce qui est à Cesar et laisse Doraki l'expliquer
Re: Le demi-sucre de Zac Haroz.
un gars qui libère la mémoire allouée avant de sortir de de son programme, ne peut pas être foncièrement mauvaisscarta a écrit: double res = prob[current+2];
free(prob);
return res;
26 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
