La boite de sucre

[Ben314]

Le problème avec 15x20 c'était juste pour dire que, par exemple, on peut remplir un AxB=60x35 avec des axb=15x20 et que dans ce cas on ni (a divise A et b divise B) ni (ab divise A ou B).
Mais pour la dimension 2, ce n'est pas une remarque trés pertinente car si on rempli un AxB avec des 15x20 alors forçément A et B sont divisibles par 5 et on peut diviser tout le monde par 5...

Sinon, l'histoire du coloriage, c'est une trés bonne piste. Je te confirme que ton petit rectangle r1xr2 ne peut pas contenir autant de case de chaque couleur... (pourquoi ?)

Cette méthode du "coloriage" est trés largement suffisante dans un "cas concret" comme celui de la "boite de sucre" où on peut "compter sur ces doigts" le nombre de couleurs dans le "petit bout qu'il reste".

On peut la "théoriser" un peut pour éviter de compter sur ces doigts (et traiter facilement les cas "non concret")...

C'est donc la dernière ligne droite....

[ffpower]

Et bien je n'utilisais pas vraiment que ab divise A, seulement que a et b divisent A, ce qui est permet de remplir des "lignes" de hauteur soit a,soit b..
Sinon,bon ben au moins tu me rassures pour le 'tit rectangle, mais il est vrai que ca pourrait être pas mal de le prouver ( si possible avec une méthode généralisable )
Bon bah vais réfléchir à ca et au cas 3d

[Doraki]

On a toujours que chacun des a,b,c doit diviser l'un des A,B,C (même argument, soit avec des intégrales de produits de sinus, soit avec des intégrales discrètes i.e. coloriages)

Si a|A, b|B, c|C, c'est facile.
Si a,b,c|A, alors A*B*C est pavable <=> B*C est pavable par (a*b) (b*c) et (a*c).
Si a,b|A et c|B alors A*B*C est pavable <= C est pavable par (a) et (b).

Y'a encore du boulot.

[Ben314]

En y regardant de plus prés, dans le cas de la dim 3 (ou plus), je ne suis pas totalement sûr d'avoir une C.N.S (a cause du problème de frobenius concernant l'écriture en combinaison linéaire à coeffs dans N)

Disons donc que je cherche une C.N.S valable pour A,B,C suffisement grands.....

Sinon, les coloriages (ou les intégrales ou les sinus....) vous y êtes presque.... il manque un "détail"... (tout bête)

[Ben314]

Bon, comme le post "s'enterre", je fait un petit point sur ce qui est "ma soluce" :
Effectivement, pour remplir une boite AxBxC avec des "allumettes" dx1x1, il faut que d divise A ou B ou C (coloriages, intégrale,...).
Donc, pour remplir une boite AxBxC avec des pavés axbxc, il faut que a,b et c divisent A ou B ou C.
De plus, en regardant ce qu'il se passe sur les faces de la boite, on voit que pgcd(a,b), pgcd(a,c) et pgcd(b,c) doivent diviser deux des nombres A,B et C.
Evidement, pgcd(a,b,c) doit diviser les trois nombres A,B et C.
Sauf erreur, si A, B et C sont "suffisement grand" (à cause des conditions à la frobenius) on a bien une C.N.S. de remplissage.

Je voulais aussi faire une remarque sur une façon assez joli de prouver le résultat :

La façon la plus élémentaire de faire la preuve pour les allumettes dx1x1 consiste à faire un coloriage avec d couleurs mais c'est un peu compliqué de conclure dans le cas général (voir post #19 de ffpower).

Pour rendre les calculs plus simples, au lieu de mettre dans la case (x,y,z) la "couleur" x+y+z [mod d] et de compter les différentes couleurs, on peut mettre dans la case (x,y,z) le complexe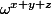 (où est une racine primitive d-ième de l'unité) puis faire la somme des valeurs des cases (qui doit être nulle) : cela devient extrêmement simple.

On peut même éviter les raisonnements sur les "faces" de la boite en mettant directement dans la case (x,y,z) le monome formel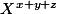 . La somme des contenu des cases recouvertes par tout pavé axbxc est alors un polynôme de la forme 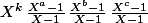avec 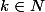donc une condition nécéssaire pour pouvoir remplir une boite AxBxC est que le polynôme divise : on retrouve ainsi toutes les conditions...

Cette dernière façon de procéder peut même être utile pour des problèmes de pavages avec des pavé différents, par exemple dans le casse-tête classique suivant :
"Déterminer toutes les façons de remplir une boite 5x5x5 avec cinq cubes 1x1x1, six pavés 1x2x4 et six pavés 2x2x3."
Ici, en utilisant la méthode ci dessus (conjoitement à d'autre raisonnements) on peut trouver des conditions assez fortes sur les positions des cinq cubes 1x1x1 avant de commencer à faire des essais...