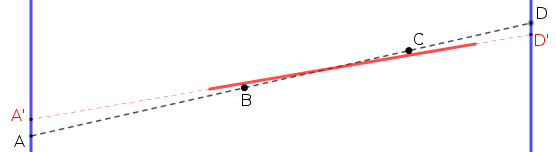
Avec le tore, ce que je regarde, c'est les droites
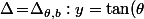x\!-\!b)
où on peut regarder

comme étant une valeur "modulo 1"
(1) vu que translater une droite de 1 vers le haut ne change rien aux problèmes de "blocages".
Une telle droite passe par un clou, c'est à dire un
)
avec
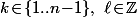
ssi
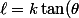\!-\!b)
c'est à dire
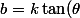)
modulo 1
(2).
La droite a donc comme équation
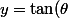(x\!-\!k))
, elle passe par le clou
)
, elle coupe les murs en

(à gauche) et en

(à droite) avec
})
et
})
ce qui signifie que,
si une de ces deux longueur est 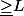 , alors le clou n'est pas un obstacle au déplacement de l'aiguille (3)
, alors le clou n'est pas un obstacle au déplacement de l'aiguille (3).
Ensuite, en regardant le géogébra, on voit que pour les petit

on peut trouver sans problème un chemin (en terme de
)
) qui va de
)
à
)
sans couper les courbes tracées par géogébra, c'est à dire en ne traversant ces courbes qu'en des endroit où on a
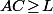
ou bien
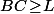
donc où on peut faire passer l'aiguille d'un coté à l'autre coté du clou
(4).
Quand on fait augmenter

, ça augmente la partie effectivement tracée des courbes
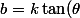)
modulo 1 et là où ça bloque, c'est lorsque pour la première fois deux courbes se mettent à avoir un point commun (autre que (0,0)) ce qui créé une composante connexe dont on ne peut pas s'échapper (... à priori...
(5)).
Arrivé là, ben c'est plus que du calcul relativement simple consistant à regarder à quel moment (en terme de valeur de

) va apparaître l'intersection entre entre deux courbes différentes

et
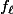
histoire de voir quelles vont être les deux première courbes à se croiser quand on augmente le curseur

.
(1) Sur le truc géogébra,

il est sur l'axe des

et la valeur de

(modulo 1) est affichée comme étant entre -1/2 et +1/2 (c'est plus joli du fait de la symétrie)
(2) Et les fonction

du géogébra, c'est les fonctions
)
modulo 1.
(3) Donc dans le géogébra, la fonction ne s’affiche que si les deux longueurs sont
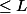
.
(4) Et jusque là, on ne se préoccupe pas des droite exceptionnelles qui passent par plusieurs clou : sur le tore en
)
, elles ne représentent que des points isolés et il y a toujours moyen de passer à coté.
(5) Là, c'est comme toi, c'est pas archi. bien formel le fait qu'on peut pas s'échaper dans ce cas là : il est clair que pour toute longueur d'aiguille inférieure à la barre que je trouve, on pourra effectivement faire demi tour (en suivant le fameux chemin en
)
), mais le fait qu'on ne peut plus au delà de cette barre devrait sans doute être détaillé.
où
.
où
maxi. tel que