La danse des fourmis
56 messages
- Page 1 sur 3 - 1, 2, 3
La danse des fourmis
Bonjour, un petit défi dont j'aime beaucoup une méthode de résolution.
Plusieurs fourmis sont sur un cercle et se déplacent à la même vitesse. Certaines tournent dans un sens et d'autres dans l'autre sens. Quand deux fourmis se rencontrent elles font demi-tour et repartent à la même vitesse.
En fonction des conditions initiales, existera t'il un moment où toutes les fourmis retrouveront exactement leur position et leur sens de déplacement d'origine ? Si possible quelle est la période de ce mouvement de l'ensemble des fourmis ?
Volontairement, je vous laisse caractériser le problème comme vous voulez en espérant qu'il n'y ait pas d’ambiguïté dans l'énoncé. On considérera toutefois que les fourmis sont ponctuelles (sans longueur) et que le demi-tour est instantané. J'espère que cela vous amusera, n’hésitez pas à faire des variantes plus simples ou plus compliquées.
PS : Cela me vient d'un collègue donc possible que ce soit déjà bien connu mais au pire cela fera peut-être découvrir à d'autres.
Plusieurs fourmis sont sur un cercle et se déplacent à la même vitesse. Certaines tournent dans un sens et d'autres dans l'autre sens. Quand deux fourmis se rencontrent elles font demi-tour et repartent à la même vitesse.
En fonction des conditions initiales, existera t'il un moment où toutes les fourmis retrouveront exactement leur position et leur sens de déplacement d'origine ? Si possible quelle est la période de ce mouvement de l'ensemble des fourmis ?
Volontairement, je vous laisse caractériser le problème comme vous voulez en espérant qu'il n'y ait pas d’ambiguïté dans l'énoncé. On considérera toutefois que les fourmis sont ponctuelles (sans longueur) et que le demi-tour est instantané. J'espère que cela vous amusera, n’hésitez pas à faire des variantes plus simples ou plus compliquées.
PS : Cela me vient d'un collègue donc possible que ce soit déjà bien connu mais au pire cela fera peut-être découvrir à d'autres.
Re: La danse des fourmis
Bonjour,
Amusant problème, j'en connaissais des variantes.
Il est intéressant de considérer la situation au bout du temps qu'une fourmi prend pour faire un tour sans rencontrer d'obstacle.
Amusant problème, j'en connaissais des variantes.
Il est intéressant de considérer la situation au bout du temps qu'une fourmi prend pour faire un tour sans rencontrer d'obstacle.
Re: La danse des fourmis
Très intéressant en effet !
Si tu en as le temps et l'envie, je serai curieuse de lire ta version. J'ai bien une manière de faire relativement visuelle, mais pour être honnête, le formalisme mathématiques s'est perdu en route.
En tout cas, si cela peut rassurer ceux qui n'osent pas essayer, à part un peu d'arithmétique, il n'y a vraiment pas besoin de connaissances particulières.
Si tu en as le temps et l'envie, je serai curieuse de lire ta version. J'ai bien une manière de faire relativement visuelle, mais pour être honnête, le formalisme mathématiques s'est perdu en route.
En tout cas, si cela peut rassurer ceux qui n'osent pas essayer, à part un peu d'arithmétique, il n'y a vraiment pas besoin de connaissances particulières.
Re: La danse des fourmis
Le problème , c'est que ce site est trop bien fait : quand on ouvre ce sujet, on voit apparaître les sujets plus ou moins similaires qui ont déjà été ouverts.
Et donc les solutions apportées à l'époque.
Et donc les solutions apportées à l'époque.
Re: La danse des fourmis
Pas trop de réponses ...
Je ne suis pas allé voir les fils précédents.
Quelques notations : d le nombre de fourmis qui tournent vers la droite, g le nombre de fourmis tournant vers la gauche, n=d+g. On numérote les fourmis de 1 à n en parcourant le cercle dans le sens des aiguilles d'une montre. Les fourmis restent toujours dans le même ordre circulaire puisqu'elles ne se croisent pas
Au bout du temps T nécessaire pour faire un tour, on retrouve globalement les fourmis aux mêmes endroits sur le cercle, allant dans la mêmes directions. Mais les numéros des fourmis ont été permutés par une puissance du cycle (1,2,...,n) - rappelons qu'elles restent dans le même ordre circulaire.
Quelle puissance ? Introduisons un observateur qui voit passer les fourmis en un point fixe du cercle. Pendant le temps T, il en voit passer d vers la droite et g vers la gauche. La puissance est donc d-g.
Les fourmis retrouveront exactement leur place de départ et leur direction de départ au bout de m fois T, où m est le plus petit entier >0 tel que m(d-g) soit multiple de n=d+g.
Je ne suis pas allé voir les fils précédents.
Quelques notations : d le nombre de fourmis qui tournent vers la droite, g le nombre de fourmis tournant vers la gauche, n=d+g. On numérote les fourmis de 1 à n en parcourant le cercle dans le sens des aiguilles d'une montre. Les fourmis restent toujours dans le même ordre circulaire puisqu'elles ne se croisent pas
Au bout du temps T nécessaire pour faire un tour, on retrouve globalement les fourmis aux mêmes endroits sur le cercle, allant dans la mêmes directions. Mais les numéros des fourmis ont été permutés par une puissance du cycle (1,2,...,n) - rappelons qu'elles restent dans le même ordre circulaire.
Quelle puissance ? Introduisons un observateur qui voit passer les fourmis en un point fixe du cercle. Pendant le temps T, il en voit passer d vers la droite et g vers la gauche. La puissance est donc d-g.
Les fourmis retrouveront exactement leur place de départ et leur direction de départ au bout de m fois T, où m est le plus petit entier >0 tel que m(d-g) soit multiple de n=d+g.
Modifié en dernier par GaBuZoMeu le 08 Fév 2021, 09:32, modifié 2 fois.
Re: La danse des fourmis
J'ai regardé le fil, leur manière de faire est très similaire par contre ils ne donnent pas la période donc l'exercice reste valable pour les (ou le) plus motivé(s).
Je suis d'accord que les fourmis auront retrouvé leur place quand tu le dis (si on précise le cas d=g) mais sauf erreur de ma part, on peut faire mieux. Ceci dit, tu démarres quand même mieux que moi, ma première approche juste pour voir si c'était périodique était n!T (j'avais vu très large )
)
Prenons un exemple pour que tout le monde visualise et servons nous des notations déjà proposées, je vais noter + et - leur sens donc on peut avoir
(1+,2-,3-,4-), elles seront de retour en 4T
(1+,2+,3-,4-), elles seront de retour en 2T
Édit : pour virer l'explication comme il y a mieux ensuite
Je suis d'accord que les fourmis auront retrouvé leur place quand tu le dis (si on précise le cas d=g) mais sauf erreur de ma part, on peut faire mieux. Ceci dit, tu démarres quand même mieux que moi, ma première approche juste pour voir si c'était périodique était n!T (j'avais vu très large
Prenons un exemple pour que tout le monde visualise et servons nous des notations déjà proposées, je vais noter + et - leur sens donc on peut avoir
(1+,2-,3-,4-), elles seront de retour en 4T
(1+,2+,3-,4-), elles seront de retour en 2T
Édit : pour virer l'explication comme il y a mieux ensuite
Modifié en dernier par Vassillia le 13 Fév 2021, 01:05, modifié 1 fois.
Re: La danse des fourmis
Bonjour à tous
Je m'étais pas mal intéressé au problème il y a quelque temps ( j'avais même proposé une version 3D que je ne parviens pas à retrouver ) . Ma façon de voir les choses ( parmi d'autres ) , les fourmis ne changent pas de sens lors des chocs mais échangent simplement leurs papiers . Il n'y a plus qu'à suivre le mouvement des papiers rythmé par celui des fourmis qui est régulier .
Imod
Je m'étais pas mal intéressé au problème il y a quelque temps ( j'avais même proposé une version 3D que je ne parviens pas à retrouver ) . Ma façon de voir les choses ( parmi d'autres ) , les fourmis ne changent pas de sens lors des chocs mais échangent simplement leurs papiers . Il n'y a plus qu'à suivre le mouvement des papiers rythmé par celui des fourmis qui est régulier .
Imod
Re: La danse des fourmis
(1+,2-,3-,4-), elles seront de retour en 4T
(1+,2+,3-,4-), elles seront de retour en 2T
Non : 2T dans le premier cas, T dans le second.
Re: La danse des fourmis
Avec ta modification, tu trouves carrément plus court que moi maintenant 
Je dois bien admettre que je n'ai rien à y redire, en tout cas je comprends nettement mieux d'où sort ta conclusion, je n'avais pas compris d'où sortait le m = ppcm (n, |d-g|) de ton message initial.
Je faisais plus ou moins comme Imod et pas moyen (pour moi) de trouver mieux que md multiple de n et mg multiple de n simultanément mais évidemment, ton résultat m|d-g| multiple de n est bien meilleur.
Je résume ce que je faisais mais je ne pense pas que ce soit améliorable :
Les fourmis + en bleu et les fourmis - en rouge portent un maillot avec un numéro pour les distinguer, à chaque fois que les fourmis se rencontrent, au lieu de faire un demi-tour, elles continuent leur chemin et échangent juste leur maillots. On peut visualiser le problème comme des fourmis rouges qui tournent vers la droite et des fourmis bleus qui tournent vers la gauche sans s’arrêter. Dès que toutes les fourmis ont réussi à retrouver leur propre maillot à la fin d'un tour, on a la période (et c'est forcément là où je fais une erreur ce qui explique que j'étais incapable de l'écrire proprement)
Chaque fourmi bleue récupére un maillot porté par une fourmi rouge avant de le redonner à la prochaine fourmi rouge rencontrée donc les g fourmis bleues vont décaler g fois les maillots portés par les fourmis rouge.
De manière similaire chaque rencontre avec une fourmi rouge retient un maillot porté par une fourmi bleue avant de le rendre à la prochaine fourmi bleue qui passe donc les d fourmis rouges vont décaler d fois les maillots portés par les fourmis bleus.
Bon ben bien joué GaBuZoMeu, c'est joli, mais sache que tu as un petit coté déprimant quand même. Cela a l'air tellement facile quand tu le fais, moi j'ai galéré sans trouver une version optimisée par contre je pensais sincèrement avoir la bonne réponse, c'est celle que mon collègue connaissait donc attendait comme quoi j'ai bien fais de poser cette énigme.
Je l'ai prévenu et il m'a dit qu'il l'avait trouvé http://www.les-mathematiques.net/phorum ... p?2,159849. C'est sans doute trop vieux pour être corrigé mais je te le dis au cas où.
Je dois bien admettre que je n'ai rien à y redire, en tout cas je comprends nettement mieux d'où sort ta conclusion, je n'avais pas compris d'où sortait le m = ppcm (n, |d-g|) de ton message initial.
Je faisais plus ou moins comme Imod et pas moyen (pour moi) de trouver mieux que md multiple de n et mg multiple de n simultanément mais évidemment, ton résultat m|d-g| multiple de n est bien meilleur.
Je résume ce que je faisais mais je ne pense pas que ce soit améliorable :
Les fourmis + en bleu et les fourmis - en rouge portent un maillot avec un numéro pour les distinguer, à chaque fois que les fourmis se rencontrent, au lieu de faire un demi-tour, elles continuent leur chemin et échangent juste leur maillots. On peut visualiser le problème comme des fourmis rouges qui tournent vers la droite et des fourmis bleus qui tournent vers la gauche sans s’arrêter. Dès que toutes les fourmis ont réussi à retrouver leur propre maillot à la fin d'un tour, on a la période (et c'est forcément là où je fais une erreur ce qui explique que j'étais incapable de l'écrire proprement)
Chaque fourmi bleue récupére un maillot porté par une fourmi rouge avant de le redonner à la prochaine fourmi rouge rencontrée donc les g fourmis bleues vont décaler g fois les maillots portés par les fourmis rouge.
De manière similaire chaque rencontre avec une fourmi rouge retient un maillot porté par une fourmi bleue avant de le rendre à la prochaine fourmi bleue qui passe donc les d fourmis rouges vont décaler d fois les maillots portés par les fourmis bleus.
Bon ben bien joué GaBuZoMeu, c'est joli, mais sache que tu as un petit coté déprimant quand même. Cela a l'air tellement facile quand tu le fais, moi j'ai galéré sans trouver une version optimisée par contre je pensais sincèrement avoir la bonne réponse, c'est celle que mon collègue connaissait donc attendait comme quoi j'ai bien fais de poser cette énigme.
Je l'ai prévenu et il m'a dit qu'il l'avait trouvé http://www.les-mathematiques.net/phorum ... p?2,159849. C'est sans doute trop vieux pour être corrigé mais je te le dis au cas où.
Re: La danse des fourmis
Le lien que tu donnes est exactement celui que je cherchais ( la recherche sur le site des Maths.net est vraiment calamiteuse ) . J'y ai raconté pas mal d'âneries à propos de la version 3D ( ou plutôt 2D sphérique ) , je ne sais pas si on peut en extraire quelque chose d'intéressant 
Imod

Imod
Re: La danse des fourmis
Trois fourmis vers la droite, une vers la gauche. Le temps se déroule de haut en bas.

L'observateur fixe voit trois fourmis passer vers la droite, une vers la gauche. Où qu'il soit, il voit que la différence entre le nombre de fourmis vers la droite et le nombre de fourmis vers la gauche est 2. Il en conclut qu'il y a un décalage de 2 vers la droite. Au bout de 2 tours, on retombe sur la situation de départ.

L'observateur fixe voit trois fourmis passer vers la droite, une vers la gauche. Où qu'il soit, il voit que la différence entre le nombre de fourmis vers la droite et le nombre de fourmis vers la gauche est 2. Il en conclut qu'il y a un décalage de 2 vers la droite. Au bout de 2 tours, on retombe sur la situation de départ.
Re: La danse des fourmis
Merci, tu m'as permis de visualiser la vraie situation (jusque là je n'y arrivais pas comme tout bouge de partout et c'est infernal à suivre). Je sais maintenant pourquoi ma transformation n'est pas bonne et c'est pire que je croyais. Je m’arrête à 3 de tes points noirs et je dis "le tour est fini" donc rien d'étonnant à ce que je mette trop de temps et que je ne donne qu'un multiple de la période.
Le nombre de collisions par tour c'est évidemment 2gd et pas gd mais sans m'en rendre compte, je n'étudie que la moitié des collisions. J'imagine que lors des collisions supplémentaires, j'aurai du modifier mon décalage de g en g-d et celui de d en d-g mais je ne suis absolument pas capable de le visualiser. De toute façon, cette idée n'a aucun intérêt par rapport à la tienne à part me donner le tourni pire que dans un manège à sensation forte, j'adopte définitivement les permutations mais au moins je sais d'où vient mon problème.
Je laisse Imod présenter ses variantes et on va essayer d'éviter de dire d'autres âneries comme il dit (c'est dingue, en cherchant, j'ai retrouvé exactement la même erreur ailleurs, on est donc plusieurs à s'être loupé de la même manière et jusque là personne ne l'avait remarqué)
Le nombre de collisions par tour c'est évidemment 2gd et pas gd mais sans m'en rendre compte, je n'étudie que la moitié des collisions. J'imagine que lors des collisions supplémentaires, j'aurai du modifier mon décalage de g en g-d et celui de d en d-g mais je ne suis absolument pas capable de le visualiser. De toute façon, cette idée n'a aucun intérêt par rapport à la tienne à part me donner le tourni pire que dans un manège à sensation forte, j'adopte définitivement les permutations mais au moins je sais d'où vient mon problème.
Je laisse Imod présenter ses variantes et on va essayer d'éviter de dire d'autres âneries comme il dit (c'est dingue, en cherchant, j'ai retrouvé exactement la même erreur ailleurs, on est donc plusieurs à s'être loupé de la même manière et jusque là personne ne l'avait remarqué)
Re: La danse des fourmis
Peut-être les gens prennent pour T le temps d'un demi-tour ?
Ça me semble plus naturel de prendre le temps d'un tour.
Ça me semble plus naturel de prendre le temps d'un tour.
Re: La danse des fourmis
C'est gentil de vouloir nous sauver la mise mais le problème est plus grave que cela. Il ne suffit pas de diviser par 2 pour que ce soit bon, enfin sur cet exemple si, mais pas systématiquement.
Moi je trouve comme Imod et comme plusieurs autres que est le plus petit entier tel que
est le plus petit entier tel que  et
et 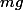 sont multiples de
sont multiples de  donc
donc }) . C'est vrai que les fourmis seront de retour à ce moment là mais elles peuvent être de retour avant comme tu l'as montré. Pour le cas où
. C'est vrai que les fourmis seront de retour à ce moment là mais elles peuvent être de retour avant comme tu l'as montré. Pour le cas où 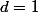 par exemple, notre resultat est mauvais si
par exemple, notre resultat est mauvais si  est impair mais bon si
est impair mais bon si  est pair.
est pair.
Plus généralement, si je ne dis pas (encore) de betises, tant que},\frac{d+g}{pgcd(d,g)})) est different de 1, on a ce facteur multiplicatif en trop. Donc je ne pense pas qu'on puisse se louper d'un facteur multiplicatif pire que 2 mais on se loupe quand même dès que
est different de 1, on a ce facteur multiplicatif en trop. Donc je ne pense pas qu'on puisse se louper d'un facteur multiplicatif pire que 2 mais on se loupe quand même dès que }) et
et }) sont tous les 2 impairs. Ce n'est pas catastrophique notre résultat pour la période mais cela reste faux.
sont tous les 2 impairs. Ce n'est pas catastrophique notre résultat pour la période mais cela reste faux.
Moi je trouve comme Imod et comme plusieurs autres que
Plus généralement, si je ne dis pas (encore) de betises, tant que
Re: La danse des fourmis
En effet , si on note  et
et  alors la période est
alors la période est  si
si 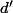 et
et  sont impairs et
sont impairs et 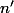 sinon . C'est un petit correctif à la solution qui méritait vraiment d'être noté . Bravo à GaBuZoMeu !!!
sinon . C'est un petit correctif à la solution qui méritait vraiment d'être noté . Bravo à GaBuZoMeu !!!
Imod
Imod
Re: La danse des fourmis
Pour en revenir aux généralisations possibles et pas trop compliquées , l'une d'entre elles semble abordable à priori .
La situation de départ est identique à celle proposée par Vassillia et le cercle des fourmis est l'équateur d'une sphère . On suppose en plus que les distances entre deux fourmis sont toutes distinctes ( pour éviter les rencontres multiples ) . Maintenant à chaque choc les fourmis tournent de 90° vers la droite et continuent leurs trajectoires à la même vitesse . Les fourmis vont donc se déplacer sur le cercle initial et sur un nombre fini de méridiens définis par les positions des chocs sur ce fameux cercle .
Le phénomène est périodique mais quel en est la période ???
Imod
La situation de départ est identique à celle proposée par Vassillia et le cercle des fourmis est l'équateur d'une sphère . On suppose en plus que les distances entre deux fourmis sont toutes distinctes ( pour éviter les rencontres multiples ) . Maintenant à chaque choc les fourmis tournent de 90° vers la droite et continuent leurs trajectoires à la même vitesse . Les fourmis vont donc se déplacer sur le cercle initial et sur un nombre fini de méridiens définis par les positions des chocs sur ce fameux cercle .
Le phénomène est périodique mais quel en est la période ???
Imod
Re: La danse des fourmis
J'ai essayé mais comme j'ai toujours autant de mal à visualiser le problème, je vais dire qu'au lieu de tourner à droite vers les poles, les fourmis font demi-tour en endossant leur cape d'invisibilité donc sans percuter personne jusqu'à ce qu'elles se croisent à nouveau où elles réapparaissent au grand jour en faisant demi-tour (j'aurai pu considérer qu'elles vont tout droit à la place avec leur cape d'invisibilité donc si vous préférez, considérez que je ne change jamais de couleur pour chaque ligne mais j'espérais me ramener au problème précédent).
Puisque tu as pris la précaution de dire qu'elles ont des distances différentes, j'en ai déduis qu'elles ne peuvent pas se percuter aux pôles donc normalement, ce modèle est équivalent.
J'ai repris l'idée de GaBuZoMeu qui m'avait bien aidée et cela se complique car pour moi, la période va dépendre d'autre chose que d et g mais de la manière dont les fourmis sont ordonnées. Je peux donner un multiple de la période mais pas la période exacte, il va falloir plus de finesse pour s'en sortir que je n'en ai pour le moment. Ci joint, mes dessins si cela peut inspirer quelqu'un en attendant.

Puisque tu as pris la précaution de dire qu'elles ont des distances différentes, j'en ai déduis qu'elles ne peuvent pas se percuter aux pôles donc normalement, ce modèle est équivalent.
J'ai repris l'idée de GaBuZoMeu qui m'avait bien aidée et cela se complique car pour moi, la période va dépendre d'autre chose que d et g mais de la manière dont les fourmis sont ordonnées. Je peux donner un multiple de la période mais pas la période exacte, il va falloir plus de finesse pour s'en sortir que je n'en ai pour le moment. Ci joint, mes dessins si cela peut inspirer quelqu'un en attendant.

Re: La danse des fourmis
En effet , tout se joue dans le plan de l'équateur et le problème est équivalent à celui où à chaque rencontre les deux fourmis deviennent transparentes pendant un demi-tour . Le mouvement des fourmis est régulier , seuls leurs états changent : visibles ou transparentes . A chaque rencontre , la règle : V+V-> T+T et dans tous les autres cas X+Y -> X+Y . La représentation de GaBuZoMeu permet de visualiser les choses mais ne met pas vraiment en relief les effets de transparence . D'un autre côté je n'ai pas de modélisation plus efficace à proposer .
A suivre donc ...
Imod
A suivre donc ...
Imod
Re: La danse des fourmis
Je pense qu'on peut préciser :
- Chaque rencontre V+V -> T+T certes
- Il y a des rencontres T+T -> V+V chaque fois que la longueur parcouru par T est la bonne (circonférence cercle/sqrt(2) sur le dessin)
En conséquence, les lignes pointillés (qui risquent de nous embêter) font des zigzags avec systématiquement la même bonne amplitude et ce sera vrai quelque soit le cas de figure.
J'ai tenté vainement de dénombrer les zigzags à problème :
- 2 points qui sont à la bonne distance peuvent définir 2 zigzags (l'un vers l'intérieur du carré que je ne compte pas comme il ne pose pas problème et l'un vers l’extérieur du carré que je compte car il peut poser problème)
- il y a dg paires de points à la bonne distance donc potentiellement dg zigzags à problème.
Je peux toujours en déduire un majorant de la période en y allant comme une sauvage à grand coup de gourdin mais je suis sure qu'on peut faire mieux. Je n'arrive pas à dénombrer proprement les zigzags à problème qui apparaissent simultanement pendant un tour et les zigzags à problème qui n'apparaissent pas du tout en fonction de la disposition initiale + ou - des fourmis.
Je lâche l'affaire jusqu'à nouvel ordre, je vais attendre une réponse éventuelle de quelqu'un ou alors de trouver une nouvelle approche.
- Chaque rencontre V+V -> T+T certes
- Il y a des rencontres T+T -> V+V chaque fois que la longueur parcouru par T est la bonne (circonférence cercle/sqrt(2) sur le dessin)
En conséquence, les lignes pointillés (qui risquent de nous embêter) font des zigzags avec systématiquement la même bonne amplitude et ce sera vrai quelque soit le cas de figure.
J'ai tenté vainement de dénombrer les zigzags à problème :
- 2 points qui sont à la bonne distance peuvent définir 2 zigzags (l'un vers l'intérieur du carré que je ne compte pas comme il ne pose pas problème et l'un vers l’extérieur du carré que je compte car il peut poser problème)
- il y a dg paires de points à la bonne distance donc potentiellement dg zigzags à problème.
Je peux toujours en déduire un majorant de la période en y allant comme une sauvage à grand coup de gourdin mais je suis sure qu'on peut faire mieux. Je n'arrive pas à dénombrer proprement les zigzags à problème qui apparaissent simultanement pendant un tour et les zigzags à problème qui n'apparaissent pas du tout en fonction de la disposition initiale + ou - des fourmis.
Je lâche l'affaire jusqu'à nouvel ordre, je vais attendre une réponse éventuelle de quelqu'un ou alors de trouver une nouvelle approche.
Re: La danse des fourmis
En effet , sous cette forme le problème est vraiment trop ouvert , la répartition des fourmis dans chaque demi-cercle étant une donnée importante . Il y a une version plus fermée du problème en supposant que les fourmis de chaque type ( même sens de rotation ) sont initialement régulièrement espacées sur l'équateur . L'évolution de la situation dépend alors uniquement de g et d mais l'étude est un peu plus complexe car il peut y avoir des chocs aux pôles .
Il faudrait regarder quelques cas simples g=1 , d= 2 ou g=2 , d=2 ... je ne l'ai pas encore fait .
Imod
Edit : pour éviter les chocs aux pôles on peut bien sûr se limiter à d et g premiers entre-eux .
Il faudrait regarder quelques cas simples g=1 , d= 2 ou g=2 , d=2 ... je ne l'ai pas encore fait .
Imod
Edit : pour éviter les chocs aux pôles on peut bien sûr se limiter à d et g premiers entre-eux .
56 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
