Le cuisinier chinois et les congruences

[Anonyme]

Je sèche complètement sur cette énigme, où, paraît-il, il faut utiliser les congruences !!! Ce mot était encore inconnu de moi hier. Quelqu'un pourrait-il m'expliquer ou me faire une démonstration ? Mille mercis

Une bande de dix-sept pirates s'est emparé d'un butin composé de pièces d'or d'égale valeur.
Ils décident de se les partager également, et de donner le reste au cuisinier chinois.
Celui-ci recevrait alors trois pièces. Mais les pirates se querellent, et six d'entre eux sont tués.
Le cuisinier recevrait alors quatre pièces. Dans un naufrage ultérieur, seuls le butin, six pirates et le cuisinier sont sauvés, et le partage donnerait alors cinq pièces d'or à ce dernier.

Quelle est la fortune minimale que peut espérer le cuisinier quand il décide d'empoisonner le reste des pirates?

[Patastronch]

Pour vulgariser :

X est congrue a R modulo Y signifie que que le reste de la division de X par Y est R.

Par exemple de la premiere phrase on peut dire que X est congrue a 3 modulo 17. (avec X la valeur de leur butin)

Cherche un cours sur les congruences pour connaitre les opérations possible entre plusieurs relations de congruences et ton enigme se résoudra assez simplement je pense.

[celge]

pas si simple que ça...

[celge]

ah, je viens de finir
je pensais que c'était plus simple que ça au début...
Il faut avoir le niveau terminale spé maths pour résoudre ce problème, ou être curieux, et bien connaitre ses formules de congruances, ainsi que le théorème de bézout, et le petit théorème de Gauss...Du moins, c'est grâce à ces formules que j'ai trouvé que la valeur minimale du butin était de 785 pieces d'or..
à confirmer...

[Anonyme]

Celge,

C'est effectivement la bonne réponse. Je te remercie car cela fait plusieurs jours que je suis dessus, mais serait-il possible que tu poste les calculs exacts que tu as fait, pour quelqu'un comme moi dont les derniers excercices de maths remontent à 10 ans ou presque. Encore merci

[freud]

déjà fait l'an dernier en spe

[Anonyme]

Moi perso, j'ai un bac+5, mais en ressources humaines, autant dire que les maths n'ont pas fait parties de mon cursus !!!

[mathador]

Cet exo est issu de mon livre de spé maths de TS !!!!! c'est un problème donc asses sympathique
Pour donner une piste à Non inscrit après les explications de Patastronch :
soit n le nombre de pièces :
n congru à 3 modulo 17
n congru à 4 modulo 11
n congru à 5 modulo 6.

C'est-à-dire que n = 17k + 3 = 11k' + 4 = 6k'' + 5 avec (k,k',k'') dans Z^3, reste à résoudre ça

Voili voilà :id:

[Galt]

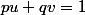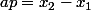Ce genre de problème est conu sous le nom de problème des restes chinois, leur énoncé est de la forme : déterminer x connaissant ses restes et modulo deux entiers premiers entre eux p et q. Pour cela, on commence par bezouter p et q, soit . On écrit ensuite , donc modulo q, que l'on multiplie par u : modulo q, et comme est congru à 1 modulo q, on a donc modulo q, donc il existe tel que , et , soit finalement, compte tenu de , .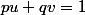
Il est facile de vérifier que les solutions obtenues conviennent.
Ce résultat sert aussi à prouver que Z /pqZ est isomorphe à Z /pZ x Z /qZ

[celge]

personnellement, j'ai fait celà avec des connaissances de terminale...en supprimant une des difficultés qui s'offrait à moi, et, apparemment, ça marche !

j'ai bien sûr commencer à déchiffrer l'énoncé, qui disait que
x = 17 k +3
x= 11 k' +4
x= 6 k'' +5

(k, k' et k'' étant des entiers relatifs)

j'ai donc trouvé 17 k +3 = 11 k' +4
d'où
17 k - 11 k' =1

comme le 17 et 11 sont premiers entre eux (pgcd (17,11) =1), on sait qu'il y'a des solutions...et l'on résout à l'aide de Bézout et de Gauss
j'ai d'abord cherché des solutions évidentes..(il y'a une methode plus longue aussi, mais , quand il y'a des solutions évidents, il est conseillé de s'en servir)

donc j'ai remarqué que 17 *2 - 11 *3 =1
donc pour k= 2 et k' =3, on verifie bien l'équation

maintenant, on peut dire que 17 *2 -11 *3 = 17 k -11 k'

d'où 17 (2- k) = 11 (3 - k')

17 et 11 étant premiers entre eux, d'après lethéorème de gauss, on peut affirmer que :

2 - k = 11 z et 3 - k' = 17 z
z étant un entier relatif

d'où k = 2 - 11 z

et k' = 3 - 17 z


ensuite, en reprenant ce que me dit l'énoncé, je peux affirmer que
6 k'' + 5 = 11 k' +4

donc que k'' = (11 k' -1) / 6

en remplaçant k' par l'expression trouvée tout à l'heure, celà donne

k'' = (-187 z +32) /6

comme k'' est entier, il faut donc que - 187 z +32 soit divisible par 6, c'est à dire un multiple de 6.

La valeur de z pour laquelle k'' est un entier (positif ici, car la valeur du trèsor est positive) le plus petit possible est -4 (en tatonnant un peu, avec les restes...une méthode très spéciale, type sytème D)

ce qui nous donne k = 46 ,k'= 71 ,k''= 130

pour ces valeurs, avec les expressions trouvées au début, on obtient
x = 785

voilà, en esperant avoir été claire, ce dont je n'ai pas vraiment l'impression...

[Alpha]

Salut à toi, Non inscrit.

J'ai la nette impression que tu crois qu'ici, on pose sa question, une âme charitable y répond, et on peut partir ailleurs et passer à autre chose sans même un mot de remerciement pour ceux qui ont eu la bonté de donner un peu de leur temps pour t'aider.

Tu as fait preuve d'une grande impolitesse :hum: . Tu n'as remercié ni Galt, ni Mathador ni Celge. C'est inacceptable. J'attends un changement d'attitude de ta part.

Nous ne sommes pas des machines à débiter des réponses.

De plus, tu n'es pas inscrit, et quand tu postes, tu ne mets même pas de nom, si bien que lorsque tu postes pour les diodes rebelles, les membres ne savent pas que c'est toi. A la place de non inscrit, mets autre chose, histoire que l'on sache à qui on parle! Et puis, Non inscrit, comme prénom, franchement, c'est nul.

Cordialement