Etudier la convergence de la suite, c'est un bon exercice de terminal + ( concours general il me semble )
Convergence dune suite
9 messages
- Page 1 sur 1
convergence dune suite
Etudier la convergence de la suite, c'est un bon exercice de terminal + ( concours general il me semble )
J'ironisais en disant "évident". Ca ne l'est pas trop. Quoique dans ces années là, j'ai vu pire au CG. Il y a eu une période de 10 ans environ (1990-2000 en gros) où les exos étaient passionnants, dans le même style que les olympiades internationales. Aujourd'hui, ils sont revenus à une formule avec de longs exercices ennuyeux.
Je laisse chercher les autres sur cet exo intéressant. A bientôt.
Je laisse chercher les autres sur cet exo intéressant. A bientôt.
Salut, j'ai trouvé qque chose pr ta question : (je trouve cet exo balaise pr un TS). Dites moi si mon raisonnement est faux par endroits.
Déjà on peut dire que (Un) est positive et ne tend pas vers 0 car on peut la minorer par (Xn) telle que Xn+1=sqrt(Xn) et X0=U0 sachant que Xn tend vers 1.
En elevant l'egalité au carré je tombe sur :
=U_{n}-\frac{1}{(n+1)^{2}})
Ensuite je calcule Un-Un+1 et je tombe sur un polynome du 2nd degres en Un+1
^{2}}))
Je trouve donc :
(n+5)}{(n+1)^{2}}))
et les deux racines sont :
(n+5)}}{n+1})
(n+5)}}{n+1})
Du coup les 2 racines convergent vers 0 avec n et comme Un ne tend par 0, a partir d'un certain rang on aura Un-Un+1>0 et donc Un est décroissante à partir d'un certain rang et donc Un converge car elle est minorée par 0.
Maintenant on pose :
et on arrive facilement à :

avec Un et Vn equivalentes vu ce qui precède.
donc on peut ecrire :

où Wn diverge vers +oo pr assurer la convergence de Vn vers une limite non nulle.
du coup on calcule Vn-sqrt(Vn) et on tombe sur :
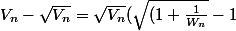)
Donc Vn et sqrt(Vn) sont equivalentes et donc Vn tend vers 1...et donc Un tend vers 1...
Voilà, merci pour ceux qui ont pris la peine de me lire. Je pense qud meme qu'il y a bcp + simple et puis je suis pas sûr de la rigueur a certains endroits.
EDIT : Sinon comment faire pr trouver un equivalent de Un - 1 ???
Re-EDIT : Aïe je viens dejà de voir une erreur : les racines ne tendent pas ttes deux vers 0, l'une tend vers 1 et l'autre vers 0...j'essaie de voir comment exploiter ceci.
En fait c'est bon : soit Un=1 : alors pour n>N on aura Un decroissante et minorée par 1 car elle ne pourra plus redevenir inférieure à 1 (la justification est assez triviale : il suffit de dire que Un>Xn avec XN=UN et Xn>1 du coup).
Déjà on peut dire que (Un) est positive et ne tend pas vers 0 car on peut la minorer par (Xn) telle que Xn+1=sqrt(Xn) et X0=U0 sachant que Xn tend vers 1.
En elevant l'egalité au carré je tombe sur :
Ensuite je calcule Un-Un+1 et je tombe sur un polynome du 2nd degres en Un+1
Je trouve donc :
et les deux racines sont :
Du coup les 2 racines convergent vers 0 avec n et comme Un ne tend par 0, a partir d'un certain rang on aura Un-Un+1>0 et donc Un est décroissante à partir d'un certain rang et donc Un converge car elle est minorée par 0.
Maintenant on pose :
et on arrive facilement à :
avec Un et Vn equivalentes vu ce qui precède.
donc on peut ecrire :
où Wn diverge vers +oo pr assurer la convergence de Vn vers une limite non nulle.
du coup on calcule Vn-sqrt(Vn) et on tombe sur :
Donc Vn et sqrt(Vn) sont equivalentes et donc Vn tend vers 1...et donc Un tend vers 1...
Voilà, merci pour ceux qui ont pris la peine de me lire. Je pense qud meme qu'il y a bcp + simple et puis je suis pas sûr de la rigueur a certains endroits.
EDIT : Sinon comment faire pr trouver un equivalent de Un - 1 ???
Re-EDIT : Aïe je viens dejà de voir une erreur : les racines ne tendent pas ttes deux vers 0, l'une tend vers 1 et l'autre vers 0...j'essaie de voir comment exploiter ceci.
En fait c'est bon : soit Un=1 : alors pour n>N on aura Un decroissante et minorée par 1 car elle ne pourra plus redevenir inférieure à 1 (la justification est assez triviale : il suffit de dire que Un>Xn avec XN=UN et Xn>1 du coup).
Si ) converge, sa limite
converge, sa limite  vérifie :
vérifie :  .
.
Mais on établit aisément par récurrence que . Il s'ensuit que 1 est la seule limite finie
. Il s'ensuit que 1 est la seule limite finie
admissible.
Supposons que la suite) est strictement croissante. Ce qui précède entraîne alors qu'elle diverge vers
est strictement croissante. Ce qui précède entraîne alors qu'elle diverge vers  . Il existe donc un entier
. Il existe donc un entier  tel que
tel que  . La fonction
. La fonction 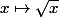 étant croissante sur
étant croissante sur  , il en résulte
, il en résulte  , ce qui est impossible car
, ce qui est impossible car  . Par conséquent, la suite
. Par conséquent, la suite ) n'est pas strictement croissante : il existe un entier naturel
n'est pas strictement croissante : il existe un entier naturel  tel que
tel que  . On a alors
. On a alors  , et par suite
, et par suite  , c'est-à-dire
, c'est-à-dire  , et ainsi de suite : la suite
, et ainsi de suite : la suite ) est décroissante à partir de l'indice
est décroissante à partir de l'indice  . On peut alors conclure à
. On peut alors conclure à  .
.
Mais on établit aisément par récurrence que
admissible.
Supposons que la suite
lol abel je regarderai plutard ce que tu as fait, je suis encore endormi la ;)
Yos jai utiliser quasiment le meme methode, on peut trouver une suite definie par reccurence qui majore Un et qui converge, Ainsi en supposant que Un est strictement croissante ( on aurait Uo > 1 obligatoirement ) on arrive par passage a la limite a une absurdité donc il existe un rang p tel que Up > U(p+1) et par reccurence => convergence vers 1 :happy3:
NB : la suite definie par reccurence qui majore Un peut etre V(n+1) = racine Vn + 1/(n+1) avec tout simplement V0>U0 ;)
Yos jai utiliser quasiment le meme methode, on peut trouver une suite definie par reccurence qui majore Un et qui converge, Ainsi en supposant que Un est strictement croissante ( on aurait Uo > 1 obligatoirement ) on arrive par passage a la limite a une absurdité donc il existe un rang p tel que Up > U(p+1) et par reccurence => convergence vers 1 :happy3:
NB : la suite definie par reccurence qui majore Un peut etre V(n+1) = racine Vn + 1/(n+1) avec tout simplement V0>U0 ;)
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
