Une belle histoire en convergence débute...
Olympiades mathématiques, énigmes et défis
-
Elerinna
- Membre Rationnel
- Messages: 559
- Enregistré le: 27 Fév 2012, 18:59
-
 par Elerinna » 14 Mar 2012, 16:11
par Elerinna » 14 Mar 2012, 16:11
Soit
 \in C^{0}(\mathbb{R}, \mathbb{R}_{+})^2, { \ } \varphi \neq \ 0)
On suppose que
dt)
converge et que

est
bornée.
Soit
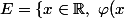 \gt 0} \)
et
)
a) Montrer que :
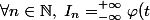 f^n(t)dt)
converge
b) Montrer que :
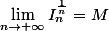
c) Montrer que :

d) On suppose que :

. Montrer que :

, et que :
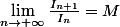
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 14 Mar 2012, 16:22
par ev85 » 14 Mar 2012, 16:22
Elerinna a écrit:Soit
 \in C^{0}(\mathbb{R}, \mathbb{R}_{+})^2, { \ } \varphi \neq \ 0)
On suppose que
dt)
converge et que f est
bornée.
Soit
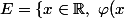 \gt 0} \)
et
)
a) Montrer que :
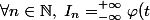 f^n(t)dt)
b) Montrer que :
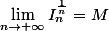
c) Montrer que :

d) On suppose que :

. Montrer que :

, et que :
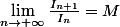
Bonjour Elerinna.
a) Euh, c'est quoi

?
-
Elerinna
- Membre Rationnel
- Messages: 559
- Enregistré le: 27 Fév 2012, 18:59
-
 par Elerinna » 14 Mar 2012, 16:30
par Elerinna » 14 Mar 2012, 16:30
ev85 a écrit:Bonjour Elerinna.
a) Euh, c'est quoi

?
Well, la définition est explicite au a). You got it.
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 14 Mar 2012, 16:35
par ev85 » 14 Mar 2012, 16:35
Elerinna a écrit:Well, la définition est explicite au a). You got it.
Ah ! dans ce cas je sais montrer le a)
e.v.
-
Elerinna
- Membre Rationnel
- Messages: 559
- Enregistré le: 27 Fév 2012, 18:59
-
 par Elerinna » 14 Mar 2012, 16:42
par Elerinna » 14 Mar 2012, 16:42
ev85 a écrit:Ah ! dans ce cas je sais montrer le a)
e.v.
Si on rédigeait ses élucubrations en encre sympathique, ce serait un apport bénéfique pour chacun. :id:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Mar 2012, 16:49
par Nightmare » 14 Mar 2012, 16:49
Je ne comprends pas qui est I(n) et ce qu'il faut montrer dans la question a).
-
Elerinna
- Membre Rationnel
- Messages: 559
- Enregistré le: 27 Fév 2012, 18:59
-
 par Elerinna » 14 Mar 2012, 17:00
par Elerinna » 14 Mar 2012, 17:00
Nightmare a écrit:Je ne comprends pas qui est I(n) et ce qu'il faut montrer dans la question a).
Mmh. A vrai dire, l'assiduité observatrice paie puisqu' une "coquille" insidieuse a commis du mimétisme... :lol3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Mar 2012, 17:18
par Nightmare » 14 Mar 2012, 17:18
La question a) n'a aucun sens telle qu'elle est écrite.
Je te propose l'exercice suivant :
Soit f une fonction continue de R dans R. Montrer que pour tout x, g(x)=f(x²).
-
Elerinna
- Membre Rationnel
- Messages: 559
- Enregistré le: 27 Fév 2012, 18:59
-
 par Elerinna » 14 Mar 2012, 17:26
par Elerinna » 14 Mar 2012, 17:26
Nightmare a écrit:La question a) n'a aucun sens telle qu'elle est écrite.
Mais si voyons. Utilise les données d'hypothèses afin d'encadrer :
 f^n(t))
puis de l'élan, conclus !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Mar 2012, 17:29
par Nightmare » 14 Mar 2012, 17:29
Mais conclure quoi? S'il y avait une question, je voudrais volontiers y répondre, mais là, je ne sais quoi dire.
-
Elerinna
- Membre Rationnel
- Messages: 559
- Enregistré le: 27 Fév 2012, 18:59
-
 par Elerinna » 14 Mar 2012, 17:33
par Elerinna » 14 Mar 2012, 17:33
Au temps pour moi de l'évidence. J'ai ajouté un mot pour que la formulation de la question prenne sens. :)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Mar 2012, 17:37
par Nightmare » 14 Mar 2012, 17:37
Nous y arrivons.
-
Elerinna
- Membre Rationnel
- Messages: 559
- Enregistré le: 27 Fév 2012, 18:59
-
 par Elerinna » 16 Mar 2012, 01:17
par Elerinna » 16 Mar 2012, 01:17
Alors aucune idée...?
Qui l'a trouvée sans risque aucun a utilisé un minorant de

sur

(ouvert).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
?