R comme C-ev ?

[Nightmare]

Hello,

une question que certains ce seront surement déjà posée :

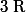
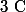
Peut-on munir d'une structure de -espace vectoriel?

[Nightmare]

Pour ceux qui n'ont pas d'idée, il faut essayer de reformuler un peu la question. Que doit-on pouvoir trouver pour munir R d'une structure de C-ev?

[ffpower]

Je ne comprend pas le sens de la question. Si on regarde R juste en tant qu'ensemble, on peut évidemment lui mettre la structure que l'on veut : on prend une bijection entre R et C par ex, et ca permet de transporter la structure de C sur R. Si c'est pas ca, j'aimerais que tu précises la question..

[Ben314]

Salut,
Déjà, à mon avis, il faut un peut "préciser" la question et demandant :
Peut on munir R d'une structure de C-espace vectoriel en conservant comme addition l'adition usuelle de R.

Edit : Grilled par ffpower...

[Nightmare]

Salut ffpower !

J'attendais une réponse comme la tienne. La question est volontairement obscure, sujette à débat.

Il est clair qu'effectivement, R et C (et C^n plus généralement) sont équipotents, donc on va pouvoir transmettre la structure de C en tant que C-ev à R. Du coup, cette question là n'est pas tellement intéressante (un minimum quand même).

Une fois ceci-dit, on peut maintenant se demander si on peut effectivement munir R d'une structure de C-ev, en demandant à ce que la loi additive corresponde à l'addition usuelle. C'est déjà un peu plus intéressant.

Edit : Grilled par Ben :lol3:

[Ben314]

Aprés, ça "sent plein pot" le :
C et R sont des Q-e.v. de "même dimension" (i.e. dénombrable) et, munir (R,+) d'une structure de C-e.v., c'est trouver une certaine fonction f:CxR->R qui soit Q bilinéaire et telle que :
a) f(1,x)=x pour tout x de R
b) f(ab,x)=f(a,f(b,x)) pour tout x de R et tout a,b de C
et je pense qu'il faut regarder ça sur des bases de R et C en temps que Q-e.v.

[Nightmare]

C'est bien l'idée Ben ! C et R étant deux Q-ev de même dimensions, ils sont isomorphes en tant que groupes additifs. On peut alors plonger C dans l'anneau des endomorphismes de R, ce qui nous permet de définir convenablement notre 2ème loi.