Bonjour mes chers frères,
çela fait 2 semaines que je pense à un problème d olympiades, je serai très reconnaissant si vous m'aidez à le résoudre:
Soit k un entier naturel impair, et n>1,
Montrez, par récurrence ,que 1*k+2*k+3*k+..........n*k est divisible par (n(n+1))/2 avec 1*k =1 à la puissance k et ainsi de suite pour les autres nombres !
Merci d avance!
Récurrence pas comme les autres
4 messages
- Page 1 sur 1
Re: Récurrence pas comme les autres
salut
soit k un naturel impair et posons = \sum_1^n i^k)
1/ déterminer une relation de récurrence entre) et
et ) du type
du type <br /> = s_k(n) + f(n))
2/ faire un raisonnement par récurrence en montrant que f(n) est multiple de n(n + 1)/2
...
soit k un naturel impair et posons
1/ déterminer une relation de récurrence entre
2/ faire un raisonnement par récurrence en montrant que f(n) est multiple de n(n + 1)/2
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Récurrence pas comme les autres
Salut,
Perso, je serais parti du fait que, pour tout entier naturel non nul k, et tout a,b réels (ou complexes) on a la factorisation donc, si k est impair,
donc, si k est impair, 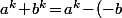^k\!=\!...) et, en particulier, si a et b sont entier (et k impair) alors
et, en particulier, si a et b sont entier (et k impair) alors 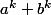 est divisible par ...
est divisible par ...
Ensuite, tu écrit (pour k impair) que
+\big(2^k\!+\!(n\!-\!1)^k\big)+\big(3^k\!+\!(n\!-\!2)^k\big)+\cdots)
mais aussi que
^k\big)+\big(2^k\!+\!(n\!-\!2)^k\big)+\cdots)
Attention : Il y a un petit piège (lequel ?)
Perso, je serais parti du fait que, pour tout entier naturel non nul k, et tout a,b réels (ou complexes) on a la factorisation
Ensuite, tu écrit (pour k impair) que
mais aussi que
Attention : Il y a un petit piège (lequel ?)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Récurrence pas comme les autres
houssamhoussni a écrit:Bonjour mes chers frères,
Bonjour frère matheux
On peut montrer que, si n est pair:
donc
De même, si n est impair
etc
On peut peut-être y arriver par récurrence, sur n ou sur k ...
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
