Une équation avec deux paramètres

[Dacu]

Bonjour à tous,

Pour quelles valeurs du paramètre réel l'équation admet une racine indépendante de ?

Cordialement,

Dacu

[chan79]

salut
Essaie avec b=2, tu as une solution "évidente", indépendante de a.

[Dacu]

salut
Essaie avec b=2, tu as une solution "évidente", indépendante de a.

Salut,

D'autres valeurs de ne sont plus?

Merci beaucoup!

[chan79]

salut

Supposons qu' un tel b existe:
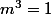
si un nombre m vérifie l'équation quel que soit a alors il la vérifie pour a=0 et ça donne et donc

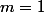
Il faut donc trouver les b tels que
quel que soit a, a(a+1)+a-a²-ab=0
2a-ab=0
a(2-b)=0
donc b=2
Et on vérifie

[Dacu]

salut

Supposons qu' un tel b existe:
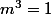
si un nombre m vérifie l'équation quel que soit a alors il la vérifie pour a=0 et ça donne et donc

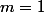
Il faut donc trouver les b tels que
quel que soit a, a(a+1)+a-a²-ab=0
2a-ab=0
a(2-b)=0
donc b=2
Et on vérifie

Salut,

Mais,si le libre terme de l'équation devient nulle, alors résulte deux racines réelles et .Le raisonnement est correct?

Cordialement,

Dacu

[chan79]

Salut,

Mais,si le libre terme de l'équation devient nulle, alors résulte deux racines réelles

Que veux-tu dire ?

[Dacu]

Salut,

Mais,si le libre terme de l'équation devient nulle, alors résulte deux racines réelles

Que veux-tu dire ?

Salut,

Retour avec:
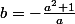
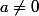
Mais,si le libre terme de l'équation devient nulle, alors résulte deux racines réelles et parce que pour avec et pour .

Cordialement,

Dacu

[chan79]

D'après ton énoncé initial, b ne dépend pas de a.

[Dacu]

D'après ton énoncé initial, b ne dépend pas de a.

Salut,

Attention, le problème ne demandez pas de trouver la valeur de telle que l'équation il doit admettre la même racine pour toute valeur de .
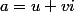
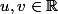
Le nombre peut être de la forme où et ?
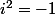
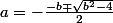
Je dis oui, parce que nous pouvons dire autrement que quel que soit le nombre .

Cordialement,

Dacu

[chan79]

Attention, le problème ne demandez pas de trouver la valeur de telle que l'équation il doit admettre la même racine pour toute valeur de .
Dacu

Salut
C'est pourtant exactement ton énoncé initial !!!
Il faut redonner l'énoncé correctement.
Cordialement