2 segments se croisent-ils ?

par **rodymary** » 05 Oct 2006, 15:46

bonjour à tous,

soit 2 segments A et B dont on connait les coordonnées x,y de chacun des points des segments.

j'aimerai savoir s'il existe une méthode simple pour savoir si ces 2 segments se croisent, autrement qu'en calculant leur equation respective, le déterminant, ...

je ne cherche pas à connaitre les coordonnées du point d'intersection, juste savoir s'il existe une intersection.

c'est pour une application informatique
merci d'avance

par **Dominique Lefebvre** » 05 Oct 2006, 16:13

Bonsoir,

La méthode la plus simple est sans doute de résoudre l'égalité entre les équations des droites qui portent les segments. Point besoin de déterminant...

Maintenant, dans un programme, tu peux aussi chercher les pixels communs aux deux segments, mais ce n'est pas forcément plus simple!

par **Flodelarab** » 05 Oct 2006, 16:16

oui.

Les intervalles des x et des y doivent avoir une partie commune.
Ensuite, prend le rectangle le plus ressérré possible sur ton point concours supposé.... tu trouveras la condition d'intersection

par **Flodelarab** » 05 Oct 2006, 16:17

rodymary a écrit:bonjour à tous,

soit 2 segments A et B dont on connait les coordonnées x,y de chacun des points des segments.

j'aimerai savoir s'il existe une méthode simple pour savoir si ces 2 segments se croisent, autrement qu'en calculant leur equation respective, le déterminant, ...

je ne cherche pas à connaitre les coordonnées du point d'intersection, juste savoir s'il existe une intersection.

c'est pour une application informatique
merci d'avance

oui.

Les intervalles des x et des y doivent avoir une partie commune.
Ensuite, prend le rectangle le plus ressérré possible sur ton point concours supposé.... tu trouveras la condition d'intersection

@Dominique: Merci de respecter l'énoncé ... pas d'equation !

par **Dominique Lefebvre** » 05 Oct 2006, 16:23

Flodelarab a écrit:oui.

Les intervalles des x et des y doivent avoir une partie commune.
Ensuite, prend le rectangle le plus ressérré possible sur ton point concours supposé.... tu trouveras la condition d'intersection

@Dominique: Merci de respecter l'énoncé ... pas d'equation !

Oui, sans doute! Mais il faut savoir dégager des solutions rapides et simples. En termes d'efficacité de calcul, connaissant les coordonnées des extrémités des segments, le calcul des deux équations et leur résolution est sans doute le plus rapide.

Ta solution suppose qu'on ait une idée du point d'intersection. Comment un programme pourrait en avoir une? A moins de commencer par un rectangle couvrant tout le domaine! Alors bof, au niveau algo, c'est pas le plus efficace...

par **Dominique Lefebvre** » 05 Oct 2006, 16:25

J'y pense, il existe une solution assez simple.

Tu traces le premier segment en mémorisant les pixels activés.
En traçant le second segment, tu vérifie si le pixel que tu veux écrire est déjà activé. Si oui, il s'agit du point d'intersection.

par **Flodelarab** » 05 Oct 2006, 16:30

Dominique Lefebvre a écrit:J'y pense, il existe une solution assez simple.

Tu traces le premier segment en mémorisant les pixels activés.
En traçant le second segment, tu vérifie si le pixel que tu veux écrire est déjà activé. Si oui, il s'agit du point d'intersection.

pffff

je reve

par **Dominique Lefebvre** » 05 Oct 2006, 16:32

Flodelarab a écrit:pffff

je reve

Pourquoi, ça marche parfaitement! et en plus tu peux tester si les deux segments sont superposés!

PS: sais-tu que c'est comme ça que fonctionnent les algo d'effacement des arêtes cachées...

par **Flodelarab** » 05 Oct 2006, 16:40

Dominique Lefebvre a écrit:Pourquoi, ça marche parfaitement! et en plus tu peux tester si les deux segments sont superposés!

PS: sais-tu que c'est comme ça que fonctionnent les algo d'effacement des arêtes cachées...

Tu ne respectes aucune des données de l'énoncé.

Personne t'as dit qu'on allait la tracer. (Puis merci l'efficacité)
On te dit de pas calculer les équations.
On te dit que tu as les coordonnées des points des segments.

si, pour le max des xmin, on pas les y dans l'ordre inverse des y pour le min des x max, alors les segments se croisent pas ... ma solution est tellement simple qu'il y a pas d'algo...

par **Dominique Lefebvre** » 05 Oct 2006, 17:06

Ouai, moi j'ai lu que c'était pour une appli informatique! Alors, si on écoutait plutôt l'utilisateur! C'est pas un énoncé de pb de cours, c'est un cahier des charges....
Et puis, je suis curieux de connaître ta manière de développer ta solution sans algo, même simple....

par **rodymary** » 06 Oct 2006, 08:46

bonjour à vous 2
effectivement je ne compte pas dessiner ou tester point par point, mon language de programmation fait ça bien plus rapidement que je ne saurais le faire.
Flodelarab, ta solution m'intéresse tout particulièrement mais je ne la comprends cependant pas bien ? peux-tu la préciser s'il te plait (ou simplifier, même si pour toi celà parait simple, je ne suis pas matheux...)
merci d'avance

par **rodymary** » 06 Oct 2006, 09:03

de manière illustrée, voici mes 2 segments :

Flodelarab, lorsque tu dis "Les intervalles des x et des y doivent avoir une partie commune." => là c'est bon, je pige, c'est après...

par **Flodelarab** » 06 Oct 2006, 14:24

rodymary a écrit:de manière illustrée, voici mes 2 segments :
Flodelarab, lorsque tu dis "Les intervalles des x et des y doivent avoir une partie commune." => là c'est bon, je pige, c'est après...

Voila le rectangle dont je parlais (celui auquel il faut se restreindre)

La droite verticale bleue est le maximum des x minimums.
La droite verticale jaune est le minimum des x maximums.
Cela permet de cerner la zone ou un chevauchement est possible.
J'appelle

l'abscisse bleue et

l'abscisse jaune.

Si les ordonnées des segments sont dans le meme ordre pour

et

alors les segments ne se croisent pas. Sinon, il se croisent.

J'ajoute, que l'on peut faire la meme chose en partant des y. Voila pkoi j'ai tracer une droite verte et un droite viollette.

ok?

par **rodymary** » 06 Oct 2006, 16:11

euh, non c'est pas beaucoup plus clair
ok pour la "plus petite boite"
quand on parle d'abscisse, c'est bien l'horizontale ?
si je comprends ton explication, ça ne marche pas, car regardes ci-dessous, j'ai inversé le sens du segment (cd)

désolé de paraître boulet mais ce n'était pas un euphémisme de dire que je n'étais pas matheux !
merci pour ta patience !

par **Flodelarab** » 06 Oct 2006, 16:14

rodymary a écrit:euh, non c'est pas beaucoup plus clair
ok pour la "plus petite boite"
quand on parle d'abscisse, c'est bien l'horizontale ?
si je comprends ton explication, ça ne marche pas, car regardes ci-dessous, j'ai inversé le sens du segment (cd)
désolé de paraître boulet mais ce n'était pas un euphémisme de dire que je n'étais pas matheux !
merci pour ta patience !

Aucun probleme.
ça marche toujours.

Si je prends l'ordre des ordonnées pour xm, j'ai [ab] au dessus de [cd] et si je prends l'ordre des ordonnées pour xM, j'ai [ab] au dessus de [cd].

Donc [ab] et [cd] ne se croisent pas ...

par **rodymary** » 11 Oct 2006, 09:33

Flodelarab a écrit:Aucun probleme.
ça marche toujours.

Si je prends l'ordre des ordonnées pour xm, j'ai [ab] au dessus de [cd] et si je prends l'ordre des ordonnées pour xM, j'ai [ab] au dessus de [cd].

Donc [ab] et [cd] ne se croisent pas ...

Bonjour et pardon pour la réponse tardive, j'étais en déplacement à l'étranger.
Tout d'abord merci pour ta patience, car je ne comprends toujours pas ton raisonnement, je ne vois pas de différence de résultat entre les 2 shémas ci-dessous ?

Shéma 1 : il n'y a pas croisement, shéma 2 : il y a croisement.
Je raisonne bien "segment" et pas "droite", on est d'accord ?
Encore merci !

par **Flodelarab** » 11 Oct 2006, 09:50

pour le dessin de gauche, (je fais l'hypothèse que tu ne retrournes pas ton écran, ni que tu marches au plafond), on observe en Xm que [AB] est en dessus de [CD]. On observe également qu'en XM, [AB] est ENCORE en dessus de [CD]

pour le dessin de droite, (je fais l'hypothèse que tu n'as pas bougé depuis la première phrase :ptdr: ), on observe en Xm que [AB] est en dessus de [CD]. On observe également qu'en XM, [AB] est en dessous de [CD]

On a changé l'ordre des segments dans celui de droite.
Donc il y a croisement dans le dessin de droite.

par **rodymary** » 11 Oct 2006, 11:33

ce que j'arrive pas à interpreter de façon mathématique (afin de le retranscrire informatiquement), c'est la notion de "en dessous" ou "au dessus" ?

par **Quidam** » 11 Oct 2006, 11:58

Plus compliqué tu meurs !

Moi, je pense que la solution proposée par Dominique est bien plus efficace...

Plus précisément. Pour clarifier l'exposé, j'appelle P et Q les extrémités du segment A, R et S les extrémités du segment B.

1 - Tu détermines l'équation de la droite contenant P et Q : soit ax+by+c=0 cette équation.

2 - Tu choisis au contraire pour la droite RS des équations paramétriques :

3 - Pour déterminer l'intersection des droites, tu remplaces x et y dans l'équation ax+by+c=0 par leur expression donnée par les équations paramétriques :

devient

Ceci donne immédiatement :

Dans les équations paramétriques,

correspond au point P, et

correspond au point Q.

Si donc le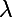

trouvé est compris entre 0 et 1, alors les deux segments se coupent. Sinon, ils ne se coupent pas !
Bien sûr, il faut vérifier que le dénominateur de l'expression ci-dessus n'est pas nul ! S'il était nul cela signifierait que les droites portant PQ et RS sont parallèles (donc éventuellement confondues, là ça devient plus compliqué). Si elles sont parallèles et distinctes, elles ne se coupent pas, a fortiori les segments portés non plus. Il reste à traiter le cas gênant où ces deux droites sont confondues...

par **Quidam** » 11 Oct 2006, 12:00

Flodelarab a écrit:On te dit de pas calculer les équations.

Personne n'a dit ça !

2 segments se croisent-ils ?

2 segments se croisent-ils ?

Qui est en ligne