Bonjour
Je m'appelle Emma et je suis en troisième.
Je suis en difficulté sur l exercice suivant et je souhaiterai avoir de l'aide svp.
"existe t il un nombre entier tel que le reste de la division de ce nombre par 2,3,4,5,6,7,8,9 est toujours égal à 1?
Je vous remercie pour votre aide.
Emma
Nombre entier / niveau 3ème
6 messages
- Page 1 sur 1
Re: Nombre entier / niveau 3ème
Salut !
Cela revient à trouver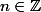 vérifiant les huit conditions :
vérifiant les huit conditions : 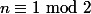 , ...,
, ..., 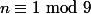 .
.
Commence déjà par déterminer l'ensemble des entiers
des entiers 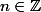 tels que
tels que 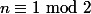 .
.
Ensuite, déterminer l'ensemble des entiers
des entiers 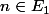 tels que
tels que 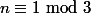 .
.
Déterminer l'ensemble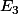 des entiers
des entiers 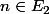 tels que
tels que 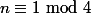 . Et ainsi de suite...
. Et ainsi de suite...
Edit : J'avais pas vu que tu étais en 3e, ne tient pas compte de mon message.
Cela revient à trouver
Commence déjà par déterminer l'ensemble
Ensuite, déterminer l'ensemble
Déterminer l'ensemble
Edit : J'avais pas vu que tu étais en 3e, ne tient pas compte de mon message.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Nombre entier / niveau 3ème
frederic1206 a écrit:Bonjour
Je m'appelle Emma et je suis en troisième.
Je suis en difficulté sur l exercice suivant et je souhaiterai avoir de l'aide svp.
"existe t il un nombre entier tel que le reste de la division de ce nombre par 2,3,4,5,6,7,8,9 est toujours égal à 1?
Je vous remercie pour votre aide.
Emma
Bonjour Emma,
Si on fait le produit 2×3×4×5×6×7×8×9 on trouve un nombre qui est divisible par 2, par 3, par 4...etc et par 9. Donc le reste de la division euclidienne de 2×3×4×5×6×7×8×9 par 2 ou 3 ou ...9 sera toujours 0 non?
Il suffit donc de faire +1 à ce nombre: le nombre 2×3×4×...×9 + 1 a pour reste 1 dans la division euclidienne par 2, par 3, par 4 ... et par9. En effet si N=2×3×4×5×6×7×8×9+1
Alors N = 2×(3×4×5×6×7×8×9) + 1
Ou bien N=3×(2×4×5×6×7×8×9)+1
Etc... (forme N=quotient×diviseur + reste)
Toujours on a N=2×q+R avec R=1 ou bien N=3×q'+R' avec R'=1
Bien entendu le reste 1 est plus petit que le diviseur à chaque fois.
@capitaine: inutile de faire appel aux modulos et au théorème des restes chinois: on est en 3eme ici.. et puis on demande d'en trouver un seul ... pas de les paramétrer tous :p
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Nombre entier / niveau 3ème
avec un tableur :
en première colonne : les nombres
en seconde colonne = "mod(A1,2)*mod(A2,3*.."
mod donnant le reste de l division euclidienne
le seul cas où le calcule vaut 1, c'est quand tous les restes de division valent 1
NB : on peut remarquer que tester 5,6,7,8,9 suffit car si par exemple le reste de la division euclidienne par 9 est 1, c'est 1 par la division par 3
en classe ensuite les colonne par ordre croissant, on cherche le premier 1.
Il faut dès le départ faire une colonne d'au moins 2600 chiffres
en première colonne : les nombres
en seconde colonne = "mod(A1,2)*mod(A2,3*.."
mod donnant le reste de l division euclidienne
le seul cas où le calcule vaut 1, c'est quand tous les restes de division valent 1
NB : on peut remarquer que tester 5,6,7,8,9 suffit car si par exemple le reste de la division euclidienne par 9 est 1, c'est 1 par la division par 3
en classe ensuite les colonne par ordre croissant, on cherche le premier 1.
Il faut dès le départ faire une colonne d'au moins 2600 chiffres
Re: Nombre entier / niveau 3ème
Bonsoir
Je n'ai pas tout compris et je vais regarder tout cela dans le détail mais merci à vous trois d'avoir répondu aussi rapidement à ma demande.
Cela est rassurant d'avoir de l'aide lorsque nous sommes perdus...
Merci beaucoup
Emma
Je n'ai pas tout compris et je vais regarder tout cela dans le détail mais merci à vous trois d'avoir répondu aussi rapidement à ma demande.
Cela est rassurant d'avoir de l'aide lorsque nous sommes perdus...
Merci beaucoup
Emma
Re: Nombre entier / niveau 3ème
Bonsoir
Ma réponse est la plus simple à comprendre quand on est au collège.. commence par ça
Ma réponse est la plus simple à comprendre quand on est au collège.. commence par ça
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
