Mise en équation 3eme début d'année
31 messages
- Page 1 sur 2 - 1, 2
Mise en équation 3eme début d'année
Bonjour à tous,
mon fils a un DM à rendre et je souhaiterais l'aider (et non lui donner le réponse) sur un sujet mais j'avoue que je sèche un peu.
Une âme charitable pour m'aider que je puisse l'aider.
L'énoncé:
Je ne connais pas les dimensions a et b du rectangle ci-contre ("accompagné d'un dessin d'un rectangle qui n'est pas à l'échelle donc pas nécessaire d'envoyer une photo"...)
Par contre je sais que si j'ajoute à la largeur le quart de cette largeur, et si j'enlève la même quantité à la longueur, j'obtiens un carré dont l'aire vaut 1cm² de plus que l'aire du rectangle.
1. Écris une relation qui donne la longueur b en fonction de la largeur a.
2. Détermine quelles étaient les dimensions du rectangle.
Merci d'avance.
mon fils a un DM à rendre et je souhaiterais l'aider (et non lui donner le réponse) sur un sujet mais j'avoue que je sèche un peu.
Une âme charitable pour m'aider que je puisse l'aider.
L'énoncé:
Je ne connais pas les dimensions a et b du rectangle ci-contre ("accompagné d'un dessin d'un rectangle qui n'est pas à l'échelle donc pas nécessaire d'envoyer une photo"...)
Par contre je sais que si j'ajoute à la largeur le quart de cette largeur, et si j'enlève la même quantité à la longueur, j'obtiens un carré dont l'aire vaut 1cm² de plus que l'aire du rectangle.
1. Écris une relation qui donne la longueur b en fonction de la largeur a.
2. Détermine quelles étaient les dimensions du rectangle.
Merci d'avance.
Re: Mise en équation 3eme début d'année
Bonjour,
Une petite aide à la réflexion pour démarrer ...
1) a : largeur, b : longueur
Si j'ai bien tout compris ... :
j'ajoute à la largeur le quart de cette largeur :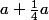
j'enlève la même quantité à la longueur :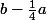
j'obtiens un carré dont l'aire vaut 1cm² de plus que l'aire du rectangle : = ab + 1 (cm²)
Une petite aide à la réflexion pour démarrer ...
1) a : largeur, b : longueur
Si j'ai bien tout compris ... :
j'ajoute à la largeur le quart de cette largeur :
j'enlève la même quantité à la longueur :
j'obtiens un carré dont l'aire vaut 1cm² de plus que l'aire du rectangle : = ab + 1 (cm²)
Re: Mise en équation 3eme début d'année
Bonjour,
Je vous remercie pour ce rapide retour.
Je voyais bien effectivement une histoire de "+ et - 1/4" dans l'équation.
Je vais essayer de "décrasser" mon cerveau de ...nous dirons quelques années...pour travailler sur cette première réflexion.
Très gentil de votre part d'aider... un jeune senior
Paco
Je vous remercie pour ce rapide retour.
Je voyais bien effectivement une histoire de "+ et - 1/4" dans l'équation.
Je vais essayer de "décrasser" mon cerveau de ...nous dirons quelques années...pour travailler sur cette première réflexion.
Très gentil de votre part d'aider... un jeune senior
Paco
Re: Mise en équation 3eme début d'année
Pas de soucis Paco !,
Par contre, je sèche également par le terme j'enlève la même quantité, il s'agit de (1/4)a ou (1/4)b .... ou ...... ?
avec (1/4)a ça n'amène à rien semble t'il .... ? Je continue à y réfléchir .....
Si d'autres collègues ont la solution .....
Par contre, je sèche également par le terme j'enlève la même quantité, il s'agit de (1/4)a ou (1/4)b .... ou ...... ?
avec (1/4)a ça n'amène à rien semble t'il .... ? Je continue à y réfléchir .....
Si d'autres collègues ont la solution .....
Re: Mise en équation 3eme début d'année
Très gentil de ta part...vraiment.
Je lis et relis l'énoncé et personnellement, j'entends par
"j'enlève la même quantité"
"j'enlève la même quantité que j'ai rajouté à la largeur" à savoir/comprendre donc (1/4)a.
Je continue également à y réfléchir... même si ce serait à mon fils d'y réfléchir... >:-(
Je lis et relis l'énoncé et personnellement, j'entends par
"j'enlève la même quantité"
"j'enlève la même quantité que j'ai rajouté à la largeur" à savoir/comprendre donc (1/4)a.
Je continue également à y réfléchir... même si ce serait à mon fils d'y réfléchir... >:-(
Re: Mise en équation 3eme début d'année
c'est pas l'esprit de l'exo mais ça m'amuse quand même.je dessine un rectangle
la largeur je la découpe en 4 = les quarts
je rajoute une bande de ce quart
j'ai maintenant 5 bandes de quart
comme j'ai enlevé une bande de quart à la longueur, c'est que le rectangle était un
4 fois le quart (de largeur) en largeur par 6 fois le quart (de largeur) en longueur(L=5 bandes de quart pour le carré +1 bande de quart = 6 bande de quart (de largeur)
déjà là on voit que c'est le bol total : 4x6= 24 le rectangle soit 25-1 du carré
sinon on peut écrire algébriquement quelle horreur d'en arriver là:
5x5x(le quart de largeur) = 4x6x(le quart de largeur) + 1
donc le quart de largeur est 1
la largeur je la découpe en 4 = les quarts
je rajoute une bande de ce quart
j'ai maintenant 5 bandes de quart
comme j'ai enlevé une bande de quart à la longueur, c'est que le rectangle était un
4 fois le quart (de largeur) en largeur par 6 fois le quart (de largeur) en longueur(L=5 bandes de quart pour le carré +1 bande de quart = 6 bande de quart (de largeur)
déjà là on voit que c'est le bol total : 4x6= 24 le rectangle soit 25-1 du carré
sinon on peut écrire algébriquement quelle horreur d'en arriver là:
5x5x(le quart de largeur) = 4x6x(le quart de largeur) + 1
donc le quart de largeur est 1
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Mise en équation 3eme début d'année
Salut,
A mon avis, ce qui vous manque surtout, c'est le "j'obtiens un carré" qui dit que a+1/4a=b-1/4a et qui permet facilement d'avoir b en fonction de a (ou le contraire).
Et la relation concernant les surfaces dit que ab+1 est égal à (a+1/4a)² (qui est bien sûr égal à (a+1/4a)x(b-1/4a) ainsi que (b-1/4a)²)
A mon avis, ce qui vous manque surtout, c'est le "j'obtiens un carré" qui dit que a+1/4a=b-1/4a et qui permet facilement d'avoir b en fonction de a (ou le contraire).
Et la relation concernant les surfaces dit que ab+1 est égal à (a+1/4a)² (qui est bien sûr égal à (a+1/4a)x(b-1/4a) ainsi que (b-1/4a)²)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Mise en équation 3eme début d'année
Salut Ben314, et mon
5x5x(le quart de largeur) = 4x6x(le quart de largeur) + 1
c'est bien?
5x5x(le quart de largeur) = 4x6x(le quart de largeur) + 1
c'est bien?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Mise en équation 3eme début d'année
zut manque des carrés, non?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Mise en équation 3eme début d'année
alors
5x5x(le quart de largeur)² = 4x6x(le quart de largeur)² + 1
sacré 1x1!
5x5x(le quart de largeur)² = 4x6x(le quart de largeur)² + 1
sacré 1x1!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Mise en équation 3eme début d'année
Bon alors je suis admis en milieu de troisième ou pas?Si c'est bon pour le début de troisième!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Mise en équation 3eme début d'année
Moi, ton raisonnement il me va parfaitement.
Pour que ce soit plus clair, j'aurais éventuellement donné un nom (style ) au quart de la largeur, mais vu qu'il y a rien de compliqué comme équation, c'est pas super utile.
) au quart de la largeur, mais vu qu'il y a rien de compliqué comme équation, c'est pas super utile.
Pour que ce soit plus clair, j'aurais éventuellement donné un nom (style
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Mise en équation 3eme début d'année
Ben314 a écrit:Salut,
A mon avis, ce qui vous manque surtout, c'est le "j'obtiens un carré" qui dit que a+1/4a=b-1/4a et qui permet facilement d'avoir b en fonction de a (ou le contraire).
Et la relation concernant les surfaces dit que ab+1 est égal à (a+1/4a)² (qui est bien sûr égal à (a+1/4a)x(b-1/4a) ainsi que (b-1/4a)²)
Bonjour Ben,
Merci également pour ton aide bien que la, j'avoue être un peu largué...
ab+1 est égal à (a+1/4a)² (qui est bien sûr égal à (a+1/4a)x(b-1/4a) ainsi que (b-1/4a)²)
Je comprends bien que ab+1=a+1/4a)x(b-1/4a) mais j'avoue ne pas comprendre le passage entre parenthèse (que j'ai mis en gras) qui est très probablement + ou - clair lorsque l'on "beigne" dedans mais en ce qui me concerne, ca remonte à.... Pfffuiiiii je préfère même pas en parler..
J'essaie donc de comprendre pour pouvoir l'expliquer à mon fils...le but étant, comme tu l'auras compris, de lui faire comprendre un raisonnement et non lui donner la réponse toute faite, ce qui n'aurait aucun sens et ne serait pas très instructif pour lui.
Si tu as le temps de développer un peu ton raisonnement que j'essaie de comprendre moi même, ce serait cool.
Merci en tous cas pour vos aides et échanges.
Paco
Re: Mise en équation 3eme début d'année
Ca vient simplement du fait que juste au dessus, on avait vu qu'on a a+1/4a=b-1/4a (= coté du carré).
Donc à n'importe quel endroit où apparait du a+1/4a, tu peut le remplacer par du b-1/4b vu que ça a la même valeur. Par exemple (a+1/4a)²=(b-1/4a)² et, si on veut on peut aussi écrire que
(a+1/4a)² = (a+1/4a)x(a+1/4a) = (a+1/4a)x(b-1/4a)
C'est la même chose que d'écrire par exemple que, si A=3 alors A²=3A=3².
Donc à n'importe quel endroit où apparait du a+1/4a, tu peut le remplacer par du b-1/4b vu que ça a la même valeur. Par exemple (a+1/4a)²=(b-1/4a)² et, si on veut on peut aussi écrire que
(a+1/4a)² = (a+1/4a)x(a+1/4a) = (a+1/4a)x(b-1/4a)
C'est la même chose que d'écrire par exemple que, si A=3 alors A²=3A=3².
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Mise en équation 3eme début d'année
Donc on obtiendrait, si je ne me suis pas trompé dans les calculs, que 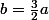 ?
?
Re: Mise en équation 3eme début d'année
laetidom a écrit:Donc on obtiendrait, si je ne me suis pas trompé dans les calculs, que?
Je répondrai ensuite à Ben mais en ce qui concerne ta réponse, moi j'aurais dit que b=a+1/2a
explication:
a+1/4a=b-1/4a
a+1/4a +1/4a=b-1/4a +1/4a (pour isoler "b", j'ajoute + 1/4a à droite ce qui annule le "-1/4a", et comme c'est une équivalence, j'ajoute également + 1/4a de l'autre coté de l'égalité, ce qui donne...)
a+1/4a+1/4a=b
a+1/2a=b
 Quoi que tu en penses ?? Ca semble cohérent !?
Quoi que tu en penses ?? Ca semble cohérent !?Paco
Re: Mise en équation 3eme début d'année
Ben314 a écrit:Ca vient simplement du fait que juste au dessus, on avait vu qu'on a a+1/4a=b-1/4a (= coté du carré).
Donc à n'importe quel endroit où apparait du a+1/4a, tu peut le remplacer par du b-1/4b vu que ça a la même valeur. Par exemple (a+1/4a)²=(b-1/4a)² et, si on veut on peut aussi écrire que
(a+1/4a)² = (a+1/4a)x(a+1/4a) = (a+1/4a)x(b-1/4a)
C'est la même chose que d'écrire par exemple que, si A=3 alors A²=3A=3².

Désolé, c'est nerveux



Comme quoi, il est primordial de lire (relire..rerelire..) un énoncé et bien le comprendre avant de se lancer dans les calculs..
"je sais que si j'ajoute à la largeur le quart de cette largeur, et si j'enlève la même quantité à la longueur, j'obtiens un carré"
les cotés d'un carré étant identiques (c'est profond ce que j'ai écris là
Et donc, pour répondre à la première question , b est il égal à "a+1/2a" !???

Très sincèrement, un Grand Merci pour votre temps passé à m'aider...
Paco
Re: Mise en équation 3eme début d'année
Bonsoir,
Avez-vous au final trouvé les dimensions a et b du rectangle ?
Pour votre question "b est il égal à "a+1/2a" ? La réponse est oui, mais vous pouvez simplifier car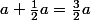 , vous obtenez donc
, vous obtenez donc 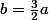
Avez-vous au final trouvé les dimensions a et b du rectangle ?
Pour votre question "b est il égal à "a+1/2a" ? La réponse est oui, mais vous pouvez simplifier car
Re: Mise en équation 3eme début d'année
triumph59 a écrit:Bonsoir,
Avez-vous au final trouvé les dimensions a et b du rectangle ?
Pour votre question "b est il égal à "a+1/2a" ? La réponse est oui, mais vous pouvez simplifier car, vous obtenez donc
Bonsoir Triumph,
Non ! J'avoue que je ne vois pas/ne comprends pas comment on peut trouver des dimensions ...sans aucune valeur..

Re: Mise en équation 3eme début d'année
Sans autre indication, et si 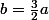 , pour trouver des dimensions il suffit de fixer arbitrairement, d'autorité, une dimension pour obtenir l'autre, car en l'état, je ne vois pas autre chose . . .
, pour trouver des dimensions il suffit de fixer arbitrairement, d'autorité, une dimension pour obtenir l'autre, car en l'état, je ne vois pas autre chose . . .
31 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
