Dm de maths sur le calcul littéral factoriser

[jeannettemaths]

Coucou!

Je n'arrive pas a factoriser pouvez vous m'aider pour les expression suivante?

1- 0,25x² + x +1

2-(6x-8)² - (2x-3)²

3-(2x+5)²-81

4-(2x+7)²-64

Merci d'avance

[WillyCagnes]

Coucou

1- 0,25x² + x +1
de la forme (a+b)²
a=0,5x et b=1

2-(6x-8)² - (2x-3)²
de la forme A²-B²=(A+B)(A-B)

3-(2x+5)²-81
de la forme A²-B²=(A+B)(A-B)

4-(2x+7)²-64
de la forme A²-B²=(A+B)(A-B)

[jeannettemaths]

Coucou

1- 0,25x² + x +1
de la forme (a+b)²
a=0,5x et b=1 Ou est passé le x² ?

2-(6x-8)² - (2x-3)²
de la forme A²-B²=(A+B)(A-B) Donc si je comprends bien on fais (6x-8)+(2x-3)) (6x-8)+(2x- 3)

3-(2x+5)²-81
de la forme A²-B²=(A+B)(A-B) Donc 3-(2x+5)² est le A et 81 le B?

4-(2x+7)²-64
de la forme A²-B²=(A+B)(A-B)

Donc (2x+7)² es le A et 64 le B?

[mathelot]

Donc (2x+7) est le A et 8 le B?

..............................

[jeannettemaths]

..............................

Mais ou va le ²?

[mathelot]

Mais ou va le ²?

il se répartit sur A+B et A-B qui ne sont pas des expressions quadratiques

[mathelot]

ça m'a donné une idée pour calculer une racine carrée.
par exemple avec 256 qui est le carré de 16

on pose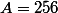 et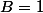



on cherche

on résout le système 2x2






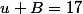
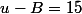
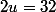
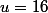
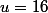est bien la racine de 256

[jeannettemaths]

il se répartit sur A+B et A-B qui ne sont pas des expressions quadratiques

Ah d'accord merci :id:

[WillyCagnes]

1- 0,25x² + x +1 =(0,5x+1)²
de la forme (a+b)²
a=0,5x et b=1
a²=(0,5x)(0,5x)=0,25x²

2-(6x-8)² - (2x-3)²
de la forme A²-B²=(A+B)(A-B)
on pose A= (6x-8)
B=(2x-3)

on obtient [(6x-8) +(2x-3)][(6x-8)-(2x-3)]
(8x-11)(4x-5)


3-(2x+5)²-81
de la forme A²-B²=(A+B)(A-B)
A=(2x+5)
B=9

4-(2x+7)²-64
de la forme A²-B²=(A+B)(A-B)
A=(2x+7)
B=8

[jeannettemaths]

1- 0,25x² + x +1 =(0,5x+1)²
de la forme (a+b)²
a=0,5x et b=1
a²=(0,5x)(0,5x)=0,25x²

2-(6x-8)² - (2x-3)²
de la forme A²-B²=(A+B)(A-B)
on pose A= (6x-8)
B=(2x-3)

on obtient [(6x-8) +(2x-3)][(6x-8)-(2x-3)]
(8x-11)(4x-5)


3-(2x+5)²-81
de la forme A²-B²=(A+B)(A-B)
A=(2x+5)
B=9

4-(2x+7)²-64
de la forme A²-B²=(A+B)(A-B)
A=(2x+7)
B=8

Merci beaucoup. Pour celle ci : 5) (5x-8)²(5x-8) la forme qu'il faut utiliser est A²-B²=(A+B) (A-B) ou le facteur commun?

[WillyCagnes]

prend donc tes lunettes...
5) (5x-8)²(5x-8) tu as un produit de facteurs différent de (5x-8)² - (5x-8)

donc
5) (5x-8)²(5x-8) =(5x-8)(5x-8)(5x-8)=(5x-8)^3

[jeannettemaths]

prend donc tes lunettes...
5) (5x-8)²(5x-8) tu as un produit de facteurs différent de (5x-8)² - (5x-8)

donc
5) (5x-8)²(5x-8) =(5x-8)(5x-8)(5x-8)=(5x-8)^3

C'est ce que je pensais mais comme j'ai du mal en maths j'ai toujours peur de me tromper... En tout cas merci

[WillyCagnes]

c'est bien continue à faire encore des exos pour bien maitriser tout ça... et reviens nous voir sur le forum

[jeannettemaths]

c'est bien continue à faire encore des exos pour bien maitriser tout ça... et reviens nous voir sur le forum

D'accord merci!