Je suis en 4ème. J'ai un devoir maison, j'ai commencé à travailler dessus mais je bloque sur la fin. Si quelqu'un aurait le remède à mon problème :id:
Voici l'énoncé :
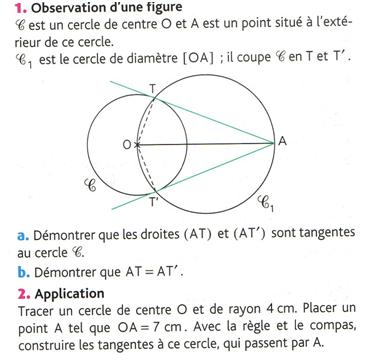
1 / On sait que C1 est le cercle de diamètre [OA], il coupe C en T et T'
Or : Définition d'une tangente
Donc AT et AT' sont tangentes au cercle C
Bon pas bon ? :doh:
2 / Dans un premier temps j'ai démontré que OTA et T'AO sont tous les deux des triangles rectangles circonscrits au cercle C1
J'ai fait la remarque que ces deux triangles circonscrits avait leur hypothénuse en commun....
J'adorerais enchainé par dire que AT = AT' mais je doute que ce soit vraiment ça ...
Merci de m'avoir lu, et merci d'avance à ceux qui auront la volonté de m'écrire :happy2:
