Géométrie - Aire d'un carré

[mellesamia]

Bonjour, pouvez-vous m'aider ? j'ai fais un exercice et je me rends compte que la correction ne concerne pas du tout ma réponse. alors est-ce que mon raisonnement est vraiment Faux ?

Vous trouverez ci-joint le sujet en question avec l'illustration.

"Dans ce problème, on s’intéresse à différentes méthodes de calcul ou d’estimation de l’aire de
certains quadrilatères.
A - Chez les Mayas
Les civilisations anciennes utilisaient divers procédés
pour estimer les aires des champs. Les Mayas, par
exemple, estimaient l'aire d'un quadrilatère en calculant
le demi-produit des longueurs des diagonales.
Aire ≈ (D×d) / 2
1. Justifier que cette estimation Maya donne la valeur exacte de l’aire d’un carré de côté a.


J'ai répondu : Un carré est une forme particulière de losange puisque, par dèfinition le losange a ses 4 cotes de meme longueur et ses diagonales sont perpendiculaires et se coupent en leurs milieux.
Le carrè est donc un losange sont les diagonales sont de meme longueur. Comme l'aire d'un losange est calculé grace a la formule (D*d)/2 ; alors l'aire d'un carré peut egalement etre calculé par cette meme formule.

Apres je fais un exemple avec un carré de 2 cm de coté
En utilisant la fomule de l'aire d'un carré c*c soit 2*2 =4
puis en utilisant la formule des Maya : soit (8*8)/2 cela me donne 3.94

j'ajoute donc la précision comme quoi cette formule n'est pas exacte.

J'ai une correction qui me parle des cotés d'un carré "Un carré ayant ses quatre côtés de même longueur et ses quatre angles au sommet droits, on peut écrire :
longueur de la diagonale au carré =a au carré + a au carré soit 2a au carré >> je ne retrouve cette formule nul part. je ne la comprends pas


Merci de votre aide.
Samia

[WillyCagnes]

bjr
J'ai une correction qui me parle des cotés d'un carré "Un carré ayant ses quatre côtés de même longueur et ses quatre angles au sommet droits, on peut écrire :
longueur de la diagonale au carré =a au carré + a au carré soit 2a au carré >> je ne retrouve cette formule nul part. je ne la comprends pas

Normal, si tu ne connais pas le Théorème de Pythagore:
Le théorème de Pythagore est un théorème de géométrie euclidienne qui met en relation les longueurs des côtés dans un triangle rectangle : le carré de la longueur de l'hypoténuse, qui est le côté opposé à l'angle droit, est égal à la somme des carrés des longueurs des deux autres côtés.

hypothenuse= diagonale du carré

d'ou Diag ² =a²+a²=2a²

https://www.cmath.fr/4eme/theoremedepythagore/cours.php
https://fr.vikidia.org/wiki/Th%C3%A9or% ... _Pythagore

[mellesamia]

Merci,

c'est très clair je connaissais les théorèmes mais je n'avais pas pensé à les utiliser.

Mais est-ce que ma réponse aurait été considéré comme bonne ou fausse ?

[pascal16]

(8*8)/2 = 3.94 est un résultat très bizarre

si la carré fait a de coté, sa diagonale est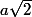

par la formule maya

[mellesamia]

Ha oui, en effet
Merci

[nodgim]

Sinon, pour un quadrilatère quelconque, le procédé maya est correct quand les diagonales sont perpendiculaires. L'erreur est d'autant plus grande que le quadrilatère est plus long que large. Il suffirait en fait de prendre les 2 hauteurs depuis une diagonale pour avoir une mesure correcte. Et c'est très simple à faire en réalisation, surtout si on veut estimer.