Bonjour,
Merci pour ce forum d'entraide !
Quelqu'un pourrait-il m'aider à factoriser ceci en m'expliquant bien les démarches svp ?
a²-19a+18
Ça ressemble à une identité remarquable mais je ne m'en sors pas. Les connaissances se sont envolées avec l'âge !
Merci beaucoup , Laurence
Factorisation
6 messages
- Page 1 sur 1
Re: Factorisation
slt,
le réflexe que la plus part des étudiants ont c'est DELTA
(pour un trinome, calculer ses racines via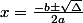
tu peux aussi factoriser à la main: avec (x+y)^2 où quand tu développes x^2 vaut a^2 (donc ici x = a) et 2xy = -19a, donc ici y = -19/2
vu que t'as un excedent (y^2) il faut le retrancher et ne pas oublier 18:
a^2-19a +18 = (a - 19/2)^2 - (19/2)^2 + 18 = (a-19/2)^2 - 289/4
et t'as une forme a^2 - b^2 que tu sais bien sûr factoriser
le réflexe que la plus part des étudiants ont c'est DELTA
(pour un trinome, calculer ses racines via
tu peux aussi factoriser à la main: avec (x+y)^2 où quand tu développes x^2 vaut a^2 (donc ici x = a) et 2xy = -19a, donc ici y = -19/2
vu que t'as un excedent (y^2) il faut le retrancher et ne pas oublier 18:
a^2-19a +18 = (a - 19/2)^2 - (19/2)^2 + 18 = (a-19/2)^2 - 289/4
et t'as une forme a^2 - b^2 que tu sais bien sûr factoriser
la vie est une fête 
Re: Factorisation
Bonjour,
Une petite astuce de derrière les fagots mais qui fonctionne (que trop souvent) consiste à chercher une racine évidente. En général, la racine évidente est un élément de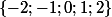 .
.
Ici en l’occurrence, vous pouvez voir que est une racine évidente (de tête) puis factoriser directement en se servant de cette information.
est une racine évidente (de tête) puis factoriser directement en se servant de cette information.
Une petite astuce de derrière les fagots mais qui fonctionne (que trop souvent) consiste à chercher une racine évidente. En général, la racine évidente est un élément de
Ici en l’occurrence, vous pouvez voir que
Re: Factorisation
Merci a vous 2 pour vos réponses !
J'avais la réponse qui était (a-1)(a-18) mais je ne savais pas comment y parvenir. La réponse de fatal_error m'en éloigne.
Je suis donc passée par les racines évidentes et j'ai obtenu le résultat !
a²-19a+18 = a²-19a+1+17
(a-1)²+17-17a
(a-1)²+17(1-a)
(a-1)²-17(a-1)
(a-1)(a-1-17)
(a-1)(a-18)
C'est bon ?
J'avais la réponse qui était (a-1)(a-18) mais je ne savais pas comment y parvenir. La réponse de fatal_error m'en éloigne.
Je suis donc passée par les racines évidentes et j'ai obtenu le résultat !
a²-19a+18 = a²-19a+1+17
(a-1)²+17-17a
(a-1)²+17(1-a)
(a-1)²-17(a-1)
(a-1)(a-1-17)
(a-1)(a-18)
C'est bon ?
Re: Factorisation
pour moi c'est correct
mis à part je vois pas trop en quoi ce que je te propose éloigne de la solution...tu as de plus fait pareil via le (a-1)^2-17a ... (idem utilisé (a+b)^2)
S = a^2-19a +18
S = (a - 19/2)^2 - (19/2)^2 + 18
S = (a-19/2)^2 - 289/4 <---- je m'étais arrêté ici, pensant que tu savais appliquer une identité remarquable pour a^2 - b^2
S = (a-19/2)^2 - (17/2)^2
S = (a - 19/2 - 17/2)(a - 19/2 + 17/2)
S = (a - 18)(a - 1)
il manquait juste les trois dernière lignes
mis à part je vois pas trop en quoi ce que je te propose éloigne de la solution...tu as de plus fait pareil via le (a-1)^2-17a ... (idem utilisé (a+b)^2)
S = a^2-19a +18
S = (a - 19/2)^2 - (19/2)^2 + 18
S = (a-19/2)^2 - 289/4 <---- je m'étais arrêté ici, pensant que tu savais appliquer une identité remarquable pour a^2 - b^2
S = (a-19/2)^2 - (17/2)^2
S = (a - 19/2 - 17/2)(a - 19/2 + 17/2)
S = (a - 18)(a - 1)
il manquait juste les trois dernière lignes
la vie est une fête 
Re: Factorisation
Ha ben oui, en effet ! J'ai pris peur quand j'ai vu les fractions et me.suis arrêtée avant ! J'avoue que ça fait plus de 30 ans que je n'ai pas joué avec les identités remarquables et mon mon cerveau est un peu rouillé.
Merci pour vos réponses et votre travail.
Merci pour vos réponses et votre travail.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 193 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
