Equation triangle

par **Mystesis** » 17 Fév 2013, 21:21

Bonsoir,
Je suis actuellement bloquée à un exercice de maths. Je précise qu'il faut faire une équation il me semble.
Voilà mon problème :

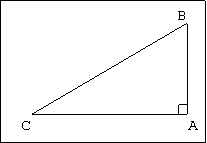
On sait que AB=28, que AC= x et que BC= x+8.
Déterminer la valeur de x.

Si quelqu'un pourrait m'aider, ne serait-ce qu'en me donnant un petit indice ça m'aidera.
Merci beaucoup, bonne soirée !

par **mcar0nd** » 17 Fév 2013, 21:28

Mystesis a écrit:Bonsoir,
Je suis actuellement bloquée à un exercice de maths. Je précise qu'il faut faire une équation il me semble.
Voilà mon problème :

On sait que AB=28, que AC= x et que BC= x+8.
Déterminer la valeur de x.

Si quelqu'un pourrait m'aider, ne serait-ce qu'en me donnant un petit indice ça m'aidera.
Merci beaucoup, bonne soirée !

Salut, ton triangle est rectangle, donc tu peux appliquer le théorème de Pythagore et tu résous l'équation que tu trouves.

par **chan79** » 17 Fév 2013, 21:28

Mystesis a écrit:Bonsoir,
Je suis actuellement bloquée à un exercice de maths. Je précise qu'il faut faire une équation il me semble.
Voilà mon problème :

On sait que AB=28, que AC= x et que BC= x+8.
Déterminer la valeur de x.

Si quelqu'un pourrait m'aider, ne serait-ce qu'en me donnant un petit indice ça m'aidera.
Merci beaucoup, bonne soirée !

salut
Pythagore

par **Suigetsu** » 17 Fév 2013, 21:29

tu sais que ABC est un triangle rectangle donc selon le théorème de Pythagore on a l'égalité suivante: BC² = AC² + AB²

ensuite tu remplace par les valeurs correspondantes puis tu résous. Pense à l'identité remarquable (a+b)² = a²+2ab+b²

par **Mystesis** » 17 Fév 2013, 21:36

Bonjour,
Merci pour vos réponses.
Donc :
Dans le triangle ABC rectangle en A, j'applique le théorème de Pythagore :
CB²= CA²+AB²
(x-8)²= 28²+x²
Mais après je peux pas continuer, donc faut que je fasse une équation ? Sinon si on peut continuer le théorème, je crois que je vais aller le réviser ahlàlà.. x)

par **mcar0nd** » 17 Fév 2013, 21:39

Mystesis a écrit:Bonjour,
Merci pour vos réponses.
Donc :
Dans le triangle ABC rectangle en A, j'applique le théorème de Pythagore :
CB²= CA²+AB²
(x+8)²= 28²+x²
Mais après je peux pas continuer, donc faut que je fasse une équation ? Sinon si on peut continuer le théorème, je crois que je vais aller le réviser ahlàlà.. x)

Attention, c'est x+8. Ensuite, tu développes avec les identités remarquables et tu résous cette équation.

par **Suigetsu** » 17 Fév 2013, 21:41

CB² = (x+8)² et pas (x-8)²

maintenant tu dois réduire chaque membre de l'équation puis la résoudre
(x+8)² = ??????
28² = ??????

par **Mystesis** » 17 Fév 2013, 21:42

Waw t'as la vue fine lol. Merci.
Développer avec les identités remarquables ?
(x+8)²= x²+2(x+8)+8² ?
Désolée je suis nulle en maths ><'

par **mcar0nd** » 17 Fév 2013, 21:43

Mystesis a écrit:Waw t'as la vue fine lol. Merci.
Développer avec les identités remarquables ?
(x+8)²= x²+2(x+8)+8² ?
Désolée je suis nulle en maths ><'

L'identités remarquable c'est

. Donc si tu reprends ton calcul, ça te donne quoi?

par **Suigetsu** » 17 Fév 2013, 21:45

(a+b)² = a²+2ab+b²

par **Mystesis** » 17 Fév 2013, 21:49

mcar0nd a écrit:L'identités remarquable c'est . Donc si tu reprends ton calcul, ça te donne quoi?

C'est bien, ce que j'ai marqué, (x+8)²= x²+2(x+8)+8², non ?
Ce qui ferait (x+8)²= x²+2x+16+64 si je ne me trompe pas.

Suigetsu > (x+8)²= x²+8²= x²+64
28²=784

[PS: Je vais dormir :lol5: ]

par **mcar0nd** » 17 Fév 2013, 21:51

Mystesis a écrit:C'est bien, ce que j'ai marqué, (x+8)²= x²+2(x+8)+8², non ?
Ce qui ferait (x+8)²= x²+2x+16+64 si je ne me trompe pas.

Suigetsu > (x+8)²= x²+8²= x²+64
28²=784

[PS: Je vais dormir :lol5: ]

Non, tu as

et l'identité remarquable c'est

, donc, dans ton cas, tu

et

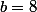
. Tu es d'accord?

par **Mystesis** » 18 Fév 2013, 07:03

Recoucou.
J'y ai repensé avant de m'endormir et je crois que je viens de repérer ma faute lol.
Je suis d'accord. Je me suis trompée pour 2ab car j'ai fait 2a+b au lieu de 2axb.
Donc ça donne : (x+8)²=x²+2*x*8+8² (les * sont les multiplications, pour pas confondre avec x).

par **Suigetsu** » 18 Fév 2013, 07:44

c'est exact

par **Mystesis** » 18 Fév 2013, 13:21

Bonjour,
Donc ça donne
(x+8)²=x²+2*x*8+8²
(x+8)²= x²+2x*8+64
(x+8)²= x²+16x+64

par **mcar0nd** » 18 Fév 2013, 13:39

Mystesis a écrit:Bonjour,
Donc ça donne
(x+8)²=x²+2*x*8+8²
(x+8)²= x²+2x*8+64
(x+8)²= x²+16x+64

Oui c'est juste ça.

par **Mystesis** » 18 Fév 2013, 17:28

Merci.
Mais est ce qu'on peut résoudre l'équation ? Parce que logiquement ça donne le même résultat des deux côtés.. Je sais pas quoi faire du coup lol. Je dois reprendre la formule du théorème de Pythagore en remplaçant ?
J'avais CB²= CA²+AB² > (x+8)²= 28²+x² tout à l'heure. En remplaçant c'est x²+16x+64 = 28²+x²
C'est ça qu'il faut faire ?

par **Suigetsu** » 18 Fév 2013, 17:40

oui maintenant tu résous en "isolant" le x.

par **Mystesis** » 18 Fév 2013, 18:13

Merci beaucoup ! Donc, ça me donne :
x²+16x+64=28²+x²
x²-x²+16x+64= 28²+x²-x²
16x+64=28²
16x+64=784
16x+64-64=784-64
16x= 720
x = 720/16
x = 45

Donc AC= 45 et BC= 45+8=54

C'est bien cela ? Si oui, merciiii j'y serais jamais arrivée sans vous lol !

par **mcar0nd** » 18 Fév 2013, 18:41

Mystesis a écrit:Merci beaucoup ! Donc, ça me donne :
x²+16x+64=28²+x²
x²-x²+16x+64= 28²+x²-x²
16x+64=28²
16x+64=784
16x+64-64=784-64
16x= 720
x = 720/16
x = 45

Donc AC= 45 et BC= 45+8=54

C'est bien cela ? Si oui, merciiii j'y serais jamais arrivée sans vous lol !

Et bah, pour moi, c'est tout juste ça. Bravo.

Equation triangle

Equation triangle

Qui est en ligne