Bonjour a tous
J'ai une citerne cylindrique d'un diamètre de 120 cm . La capacité total est de 2800 litres .
Existe t-il une formule qui me donne directement le volume restant si je connais la hauteur de liquide par rapport au fond ?
Lorsque la hauteur est de 60 cm , j'ai donc 1400 litres.
Mais lorsque j'ai 80 cm .....
Volume dans une citerne cylindrique
9 messages
- Page 1 sur 1
Le but, c'est de calculer la portion de disque qui est immergé.
Pour changer de vocabulaire, on parle de hauteur d'eau, et de longueur du cylindre.
La hauteur d'eau définit la surface (comme si un prend un disque et que jle casse a coup de pied).
Une résolution, pe pas la plus facile mais elle est intuitive:

Comme figure sur le dessin, ya une partie du disque qui est immergée. On calcule la surface joliement "hachurée" en rouge. R représente le rayon...
On sait que leq d'un cercle c'est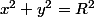
et pour nous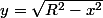
Maintenant qu'on a y=f(x), on va trouver la valeur de x du début et de x de la fin pis prendre l'intégrale f(x)dx pour trouver S/2. Par symétrie on trouve S, qui est la surface bleue et qui correspond a la surface immergée.
xdébut c'est simple, c'est -R
et...xfin c'est -R+h!
au final, on a
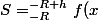dx = \bigint_{ -R}^{ -R+h} \sqrt{R^2-x^2}dx\\<br />S = R \bigint_{ -R}^{ -R+h} \sqrt{1- (\frac{x}{R})^2}dx)
Changement de variable=\frac{x}{R})
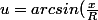\\<br />S = R \bigint_{ - arcsin(1)}^{arcsin( \frac{h-R}{R})} Rcos^2(u)du\\<br />S = R \int Rcos^2(u)du\\<br />S = R^2 \int \frac{1+cos(2u)}{2}du\\<br />S = R^2 [ \frac{u}{2}+\frac{sin(2u)}{4}]_{-arcsin(1)}^{arcsin( \frac{h-R}{R})})
Bref
 + arcsin(1)}{2} + \frac{sin(2arcsin( \frac{h-R}{R})) + sin(2arcsin(1))}{4}))
Edit : les boulettes de murphy
*Espere limiter la boulette*
Pour changer de vocabulaire, on parle de hauteur d'eau, et de longueur du cylindre.
La hauteur d'eau définit la surface (comme si un prend un disque et que jle casse a coup de pied).
Une résolution, pe pas la plus facile mais elle est intuitive:

Comme figure sur le dessin, ya une partie du disque qui est immergée. On calcule la surface joliement "hachurée" en rouge. R représente le rayon...
On sait que leq d'un cercle c'est
et pour nous
Maintenant qu'on a y=f(x), on va trouver la valeur de x du début et de x de la fin pis prendre l'intégrale f(x)dx pour trouver S/2. Par symétrie on trouve S, qui est la surface bleue et qui correspond a la surface immergée.
xdébut c'est simple, c'est -R
et...xfin c'est -R+h!
au final, on a
Changement de variable
Bref
Edit : les boulettes de murphy
*Espere limiter la boulette*
la vie est une fête 
Juste une petite remarque,
Pour trouver la surface d'une "portion de cercle", on peut aussi chercher l'angle au centre et voire la surface comme celle d'une "portion de cercle" (camembert) plus/moins celle d'un triangle isocéle (j'ai la flemme de faire un dessin...).
Cela permet de comprendre pourquoi le résultat est en "deux morceau" (et aussi cela évite l'artillerie lourde des intégrales).
Par contre ça devrait donner la même chose !!! :zen:
Pour trouver la surface d'une "portion de cercle", on peut aussi chercher l'angle au centre et voire la surface comme celle d'une "portion de cercle" (camembert) plus/moins celle d'un triangle isocéle (j'ai la flemme de faire un dessin...).
Cela permet de comprendre pourquoi le résultat est en "deux morceau" (et aussi cela évite l'artillerie lourde des intégrales).
Par contre ça devrait donner la même chose !!! :zen:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
au secours, passons a la pratique svp
bonjour, je ne suis pas matheux pour 2 sous .
j ai le meme genre de problème a régler.
voila, j'ai une cuve enterré de fioul cylindrique.de contenace 3000 litres.
lorsque qu'elle est remplie je mesure 115 cm avec une jauge.
pouvez vous me donner une formule pour que je sache combien de litre il me reste lorsque je mesure par exemple 90 ,60 cm ou x cm avec ma jauge.
merci d'avance
j ai le meme genre de problème a régler.
voila, j'ai une cuve enterré de fioul cylindrique.de contenace 3000 litres.
lorsque qu'elle est remplie je mesure 115 cm avec une jauge.
pouvez vous me donner une formule pour que je sache combien de litre il me reste lorsque je mesure par exemple 90 ,60 cm ou x cm avec ma jauge.
merci d'avance
J'ai testé les formules et j'arrive à des résultats assez bizarre , c'est à dire
que normalement ,si le niveau dans la citerne augmente de 1 cm suivant que l'on se situe dans le fond ou au milieu de la citerne la surface n'augmente pas de la même manière , or avec les formules que vous m'avez communiqués , la surface croit linéairement ( si je ne me suis pas trompé en encodant les formules dans un tableau excel et après les avoir recontrôlé plusieurs fois).
J'ai donc suivi les recommandations de BEN314 .
Calcul d'une portion du cercle et du triangle , là c'est OK .
R : rayon de la citerne
h : hauteur de liquide
Surface d'une portion du camembert : S = R² Arccos ((R-h)/R)
Surface du triangle : R . sin(Arccos((R-h)/R)) . (R-h)
Surface du morceau : Surface du camembert - surface du triangle
soit : S = R² Arccos ((R-h)/R) -R . sin(Arccos((R-h)/R)) . (R-h) (1)
Capacité total citerne : Ct en litre
Capacité restante en fonction de h : (Ct *S)/(PI * R²)


Merci pour votre aide à tous
que normalement ,si le niveau dans la citerne augmente de 1 cm suivant que l'on se situe dans le fond ou au milieu de la citerne la surface n'augmente pas de la même manière , or avec les formules que vous m'avez communiqués , la surface croit linéairement ( si je ne me suis pas trompé en encodant les formules dans un tableau excel et après les avoir recontrôlé plusieurs fois).
J'ai donc suivi les recommandations de BEN314 .
Calcul d'une portion du cercle et du triangle , là c'est OK .
R : rayon de la citerne
h : hauteur de liquide
Surface d'une portion du camembert : S = R² Arccos ((R-h)/R)
Surface du triangle : R . sin(Arccos((R-h)/R)) . (R-h)
Surface du morceau : Surface du camembert - surface du triangle
soit : S = R² Arccos ((R-h)/R) -R . sin(Arccos((R-h)/R)) . (R-h) (1)
Capacité total citerne : Ct en litre
Capacité restante en fonction de h : (Ct *S)/(PI * R²)

Merci pour votre aide à tous
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
