Volume d'une sphéroïde prolate ayant "quelques" subtilités

[xenos]

Bonjour tout le monde,

J'espère que vous pétez la forme, pour comprendre mes questions... existentielles/mathématiques... Tout d'abord, il me semble qu'il s'agit d'une sphéroïde prolate, car c'est en 3D et que 2 des 3 axes ont la même taille. L'objectif est de calculer le volume de cette sphéroïde ayant "quelques" subtilités en 4 étapes :

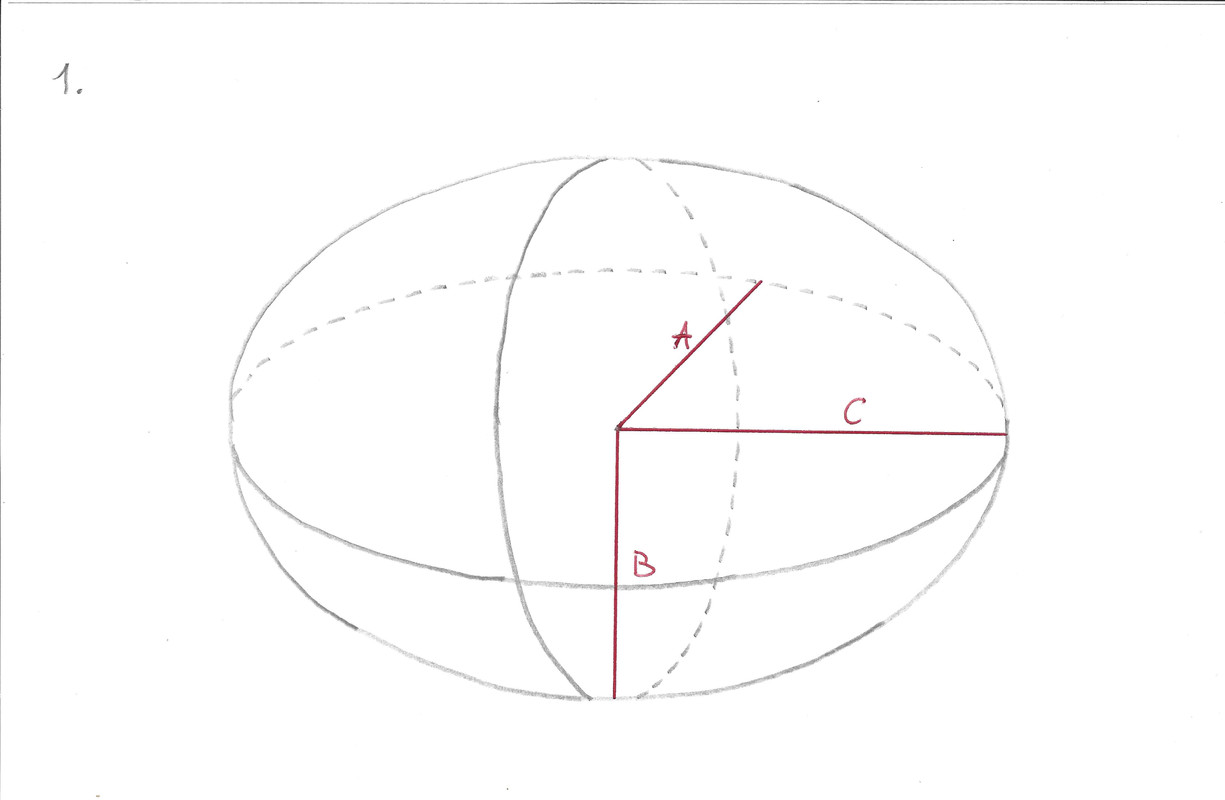
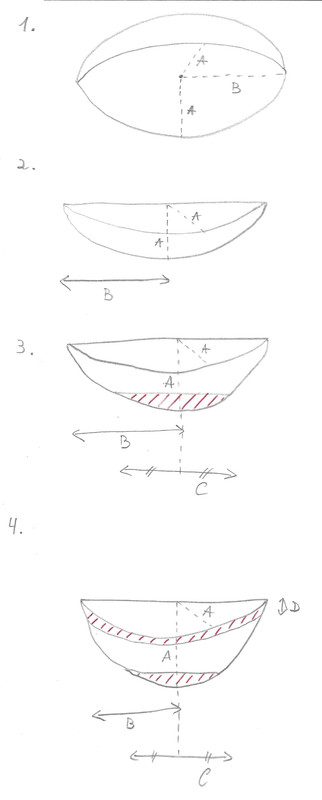
1. Le volume total de la sphéroïde se calcule par (4/3) * π * A² * B

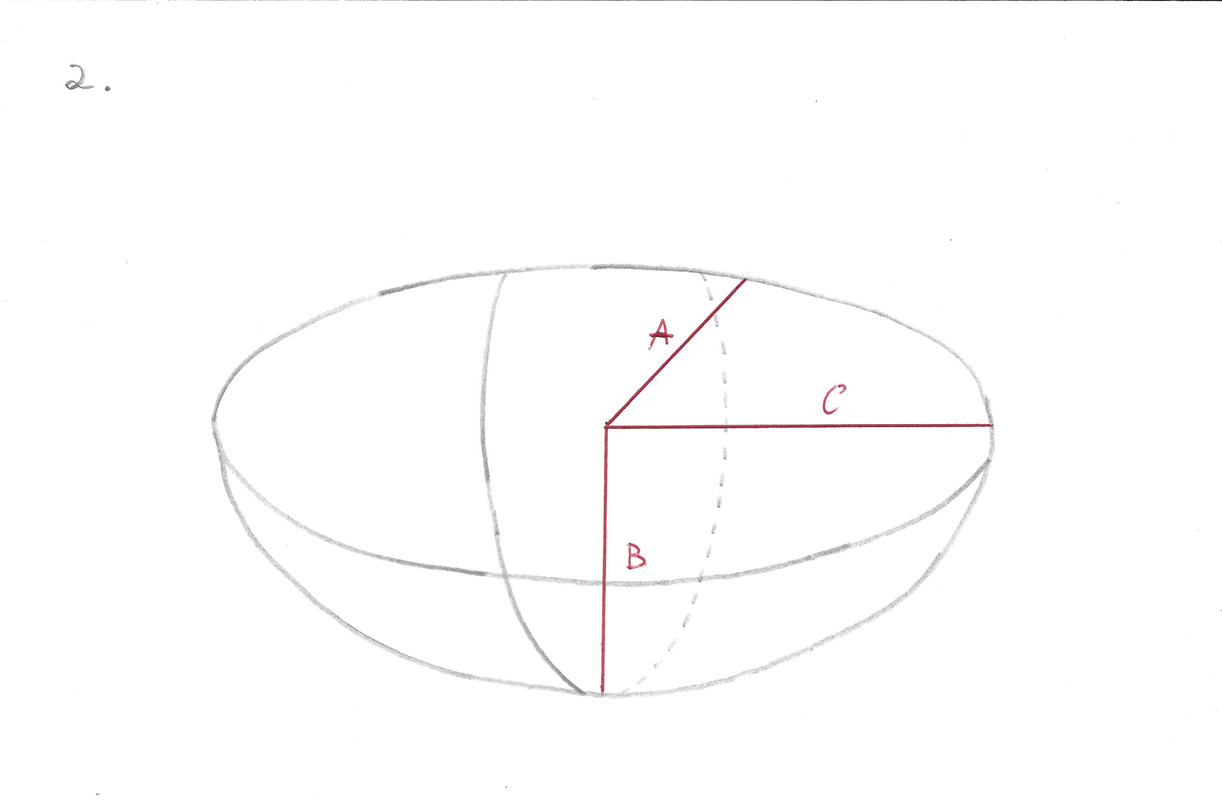
2. La sphéroïde est coupée en 2 sur l'axe le plus grand. Le volume se calcule en divisant par 2 le volume de l'étape 1.

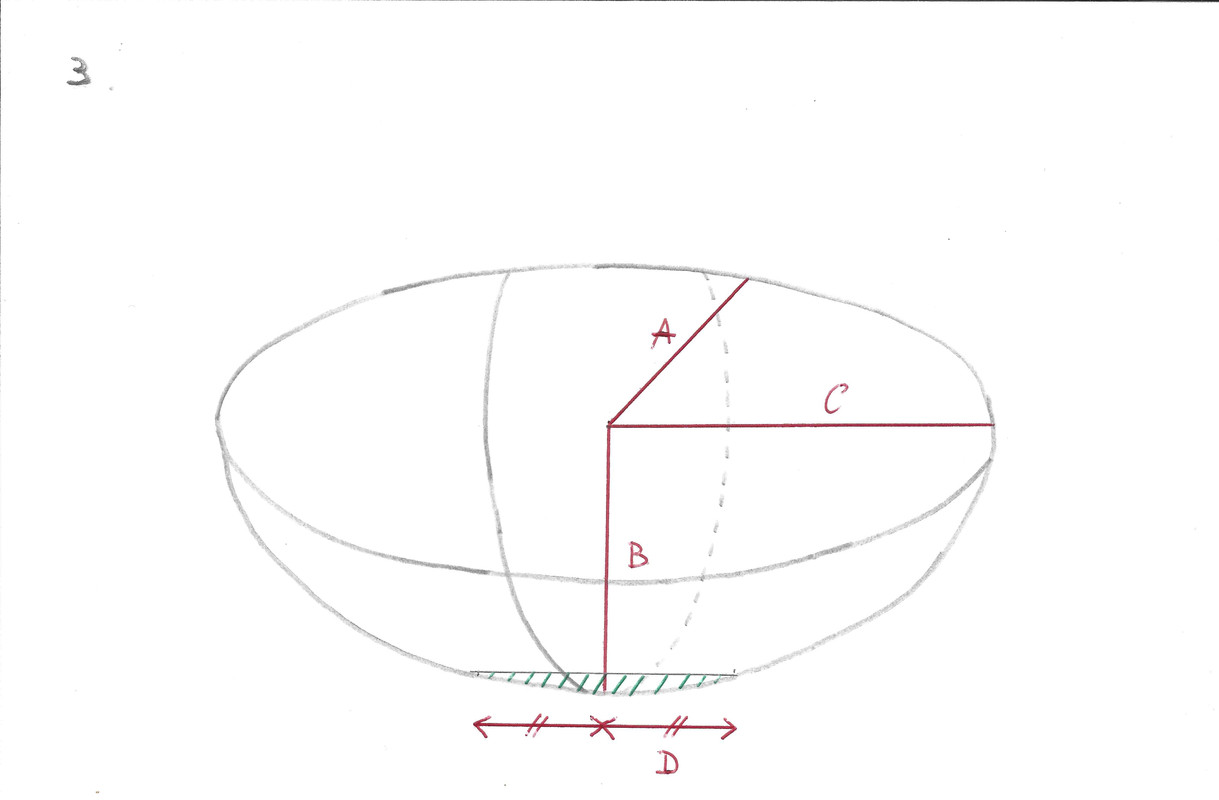
3. Imaginons que cette demi-sphéroïde est un bol, afin qu'il puisse être stable, il faut enlever le volume hachuré en rouge ayant un axe de C, qui est 1/3 de B. Puis-je partir du volume total d'une sphéroïde ayant 1 axe de longueur C ? Si oui, comment puis-je calculer les 2 autres axes ?

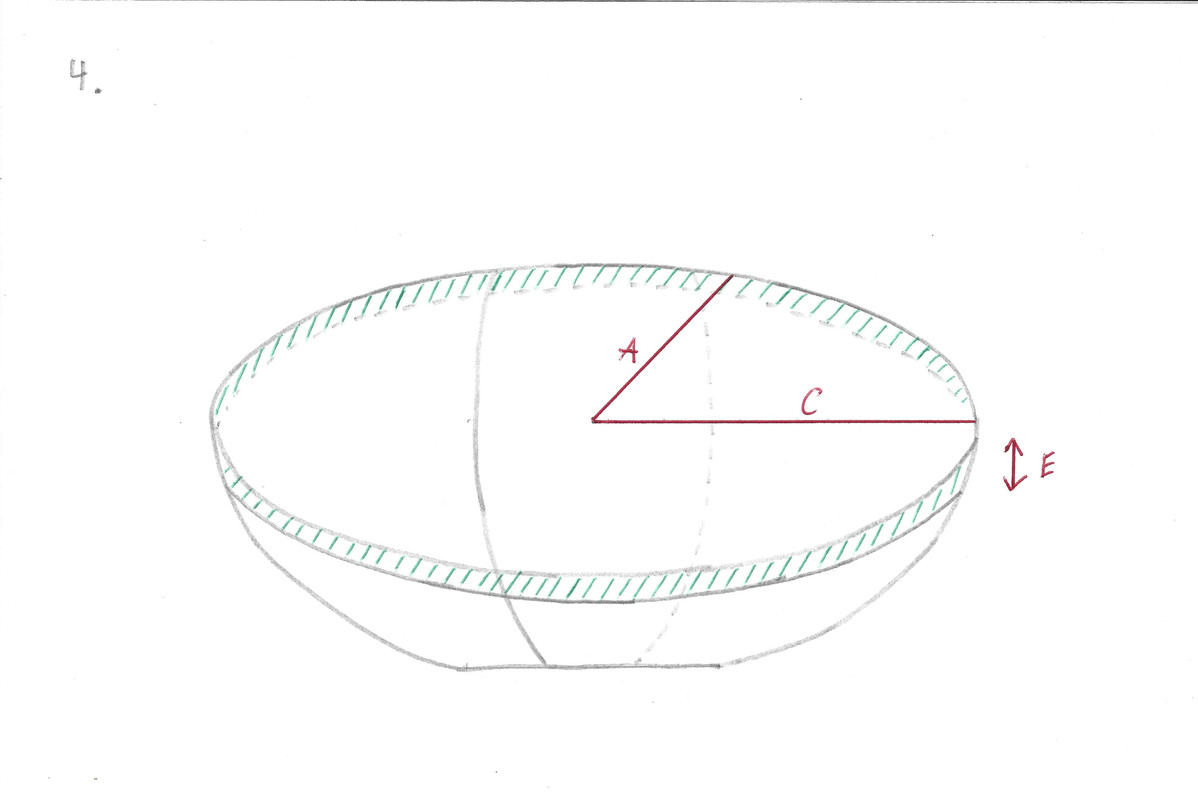
4. Gardons l'idée du bol, on ne peut pas le remplir jusqu'à ras bord, car en le bougeant le liquide coulera de tous les côtés. Je dois enlever le volume correspondant à la hauteur D. Puis-je partir du volume total d'une sphéroïde ayant l'axe A' d'une longueur A - D ? Si oui, quel est la longueur de B' ?



D'avance merci pour votre aide pour atténuer mon mal de tête !

xenos

[Ben314]

Salut,
Si j'en crois la définition donnée par Wiki., un "sphéroïde", désigne ce qui a "une forme proche de la sphère" et j'espère que tu te doute que c'est pas avec une telle définition qu'on risque de faire un quelconque début de calcul . . .
Est-ce que, éventuellement, ton sphéroïde ne serait pas un ellipsoïde de révolution (ce qui colle avec la formule que tu donne pour le volume) ?
Si c'est le cas, en se basant sur ton dessin 1 et avec l'axe des X vers la droite, celui des Y vers le haut et celui des Z vers l'arrière, l'équation de ton ellipsoïde (plein) est et ta coupe restreint à .
Quand on coupe par un plan on obtient une ellipse d'axes et donc d'aire ce qui s'intègre on ne peut plus facilement pour obtenir le volume d'une "portion" de l'ellipsoïde.
Par exemple, si je comprend correctement ton dessin 3, tu veut couper de façon à avoir (connu) ce qui correspond à couper en et le volume que tu as enlevé, c'est que je te laisse calculer.
Exactement le même raisonnent pour ton dessin 4 où, cette fois, tu as simplement coupé en et où le volume enlevé est (que je te laisse aussi calculer...)

P.S. Et il est complètement évident que ce que tu enlève dans le dessin 3, ce n'est pas un demi ellipsoïde ayant un axe égal à vu qu'au bord du truc que tu enlève, les plans tangents ne sont pas du tout verticaux alors que c'est forcément le cas pour un demi ellipsoïde coupé suivant les axes.

[xenos]

Merci Ben314 pour ta réponse,

Si c'est le cas, en se basant sur ton dessin 1 et avec l'axe des X vers la droite, celui des Y vers le haut et celui des Z vers l'arrière

Donc, A et B venant de mon schéma et X, Y et Z venant de ta formule, ça donnerait :

• 
• 

l'équation de ton ellipsoïde (plein) est

Donc la formule pour calculer le volume de l'étape 1. serait celle que tu écris ? Dès lors en remplaçant ces valeurs dans ta formule, on obtiendrait :

1. 
2. 
3. 

De toute évidence, il y a quelque chose qui m'échappe...

[xenos]

Je n'ai pas tout compris Ben314, du coup je vais essayer d'y aller étape par étape et n'hésites pas à me dire où je me trompe.



Étape 1


A = B = 6 cm
C = 9 cm

On a une sphéroïde complète dont le volume est égale à :

• 
• 
• 
• 

Étape 2


On a une demi-sphéroïde coupée en 2, où il ne reste plus que la partie inférieure. Ce volume se calcule par le volume de l'étape 1 divisé par 2, soit 678,58 cm³.



Étape 3


D = 1/3 * C = 3 cm

On supprime la partie inférieure de la demi-sphéroïde, hachurée en vert, afin qu'elle puisse tenir à plat. C'est la partie inférieure du bol. Il faut donc enlever ce volume du volume calculé à l'étape 2.

Concrètement, comment puis-je utiliser la formule que tu donnes ? Où puis-je trouver les valeurs de X, Y et Z ?



Étape 4


E = 2 cm

Le bol ne peut pas être rempli au maximum, il faut laisser la partie hachuré en vert sans liquide. Il faut donc enlever ce volume du volume de l'étape 3.

[lyceen95]

Tu connais la formule pour une sphère :
Mais est-ce que tu sais prouver ce résultat ? Est-ce que tu sais que c'est le résultat d'une certaine intégrale ?
Est-ce que le terme intégrale, ça te parle ?
Pour une sphère complète, ou une 'sphéroïde' complète, on doit calculer une certaine intégrale pour z entre -1 et 1
Quand on prend la moitié, on prend en fait une intégrale pour z entre -1 et 0.
Quand on enlève la partie hachurée en rouge, on calcule toujours la même intégrale, mais pour z entre -0.9 (valeur à ajuster) et 0.
Et quand on enlève la partie hachurée en vert, on calcule toujours la même intégrale, mais pour z entre -0.9 (valeur à ajuster) et -0.05 (valeur à ajuster, -E/B).