Vidéo Youtube perturbante

[Archytas]

Salut, je suis tombé sur cette vidéo
https://www.youtube.com/watch?v=xqTWRtNDO3U
Et j'ai tendance à penser (peut-être abusivement) que c'est du grand n'importe quoi... Enfin ça me dérange pas tant que ça tous les calculs c'est juste la réalité de A qui pose problème, ça ressemble à une série mais les sommes partielles convergent pas donc bon si A existe c'est autre chose... et la somme 1+2+3+... = -1/12 semble être une conclusion assez absurde. Mais bon il dit au début qui Riemann, Ramanujan et d'autres ont utilisé cette "somme" et j'imagine donc que c'est moi qui me trompe et que tout a bien un sens. Donc ma question est : c'est quoi A ? Quelle réalité a-t-il ? Et dans quelle mesure si vous le savez, ces grands penseurs se sont servi de cette "série" ?
Si ce qu'il dit est vrai pourquoi on s'embête à étendre zêta au plan complexe si ça reste vrai d'écrire 1^z
+ 2^z + ...
Je sais pas trop si c'est le bon endroit pour en parler...
D'ailleurs j'imagine que le sujet a déjà été abordé mais je trouve pas dans la recherche du forum.

[Robot]

Oui, c'est un marronnier.

[Archytas]

Un marronnier ?

[Robot]

https://fr.wikipedia.org/wiki/Marronnier_%28journalisme%29

[Archytas]

D'acc et donc vous avez un lien où on pourrait savoir si oui ou non c'est vraiment rigoureux ou juste si vous pouvez me dire "oui" ou "non" si ça a un sens ? Comme l'histoire de 0,9999... = 1. Au début je pensais à tord que c'était n'importe quoi et je sais pourquoi c'est correct maintenant. Et là si c'est correct j'aimerais bien savoir pourquoi

[Pseuda]

Il y a forcément une erreur quelque part dans le raisonnement. Le jeu est de trouver où.

[Ben314]

Salut,
A mon sens, tel quel (*), c'est vraiment du "grand n'importe quoi" : soit on s'adresse clairement a un public capable de comprendre qu'il y a plusieurs façons définir la notion de "somme infinie" et on précise évidement de quoi on parle, soit on s'adresse a un public débutant qui n'a même pas conscience que la définition même d'une somme infinie de termes pose problème, et je trouverais très très très nettement plus utile de faire un petit truc sur la non "convergence commutative" (par exemple) histoire de montrer que, comme toujours, il faut se méfier comme la peste de l'infini.

(*) i.e. sans le moindre mot concernant le fait qu'on manipule des séries divergentes et que la notion de "somme" n'a absolument pas le sens "usuel" qu'on lui donne au Lycée ou les premières années de post-bac.

P.S. : Et il n'y a pas à proprement parler "d'erreur de raisonnement" : il y a juste à comprendre qu'il faut un bagage certain en math (grand mini une Licence actuelle) pour définir proprement différentes notions de convergence pour les séries numériques, puis pour démontrer que, sous certaines hypothèses, certaines opérations sont licites pour certaines de ces définitions.
Mais présenté tel quel, a mon sens, c'est aussi intelligent que de parler de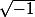 a quelqu'un qui ne sait pas encore que seuls les réels positifs ont des racines carrés réelles (ici, on parle de sommabilité dans un sens extrêmement compliqué alors qu'on s'adresse assez clairement à des personnes qui ne savent même pas ce que ça veut dire au sens "classique" du terme : déplorable...)

[Archytas]

Et donc pour en revenir à la vidéo, on est d'accord que A n'a aucun sens et qu'écrire A = 1/2 n'est pas possible puisque A n'est pas défini OU on peut donner un sens à A dans un certain cadre et dans ce cadre A vaut 1/2 ?
Comme l'a dit Robot, c'est un sujet que vous avez dû voir 1000 fois et que vous devez être lassés de relire donc un oui ou non ça existe ou pas et je vous croirai sur parole ^^ (mais dans l'hypothèse où ça existe j'aimerais beaucoup un lien si vous avez).
J'ai jeté un oeil à la convergence commutative et je ne vois pas vraiment en quoi ça aide
http://math.univ-lyon1.fr/~gelineau/devagreg/Convergence_commutative.pdf

[Ben314]

C'est la deuxième réponse : on peut donner un sens à la somme A (qui n'est évidement pas le sens usuel de limite des sommes partielles) et, dans ce cadre là, A vaut bien 1/2.

Sinon, sur le principe, ça n'a a peu prés rien a voir avec le problème de la convergence commutative.
Si je parlais de ça, c'est juste pour dire qu'à mon sens, si on doit faire passer une "vague idée" concernant les sommes infinies à un "néophyte", ça serait plutôt de montrer qu'il faut se méfier et qu'on a vite fait d'écrire n'importe quoi.

Concernant le truc de la vidéo, regarde plutôt là :
https://fr.wikipedia.org/wiki/S%C3%A9rie_divergente
dans lequel il y a un résumé rapide des différentes méthodes classiques conduisant à attribuer une valeur finie à une somme a priori divergente (avec la définition usuelle de convergente/divergente).
Ce qu'il fait (sans le dire...), c'est de considérer ce que l'article de WIKI appelle «la somme de la série zêta-régularisée».

[Archytas]

Ok ok je vois, super merci pour vos explications ! Le gars fait donc plein de trucs illégaux enfin surtout lourdement injustifiés et il les justifie rapidement sur la fin par un "vous pouvez pas comprendre", ça passe presque pour de la magie ^^... Enfin c'est comme ça que je le ressens ! Je suis content de pas avoir vu sa vidéo au moment où j'apprenais les séries, ça m'aurait vachement embrouillé je pense ! Mais bon c'est vrai qu'il dit bien que c'est un concept de somme beaucoup plus large que celui qu'on conçoit en premier abord donc il est pas vraiment attaquable ! Cela dit je pense que les gens qui voient cette vidéo retiennent surtout que "dans les maths 1+2+3+4+... = -1/12 " ce qui est assez bof .
Merci pour les éclaircissements en tout cas ! Je saurai quoi en penser maintenant

[Ben314]

..., ça passe presque pour de la magie ^^... Enfin c'est comme ça que je le ressens !

Moi aussi et c'est pour ça que j'aime pas trop...

[Doraki]

Aussi, les règles de calcul qu'il utilise sont contradictoires. On peut montrer 1=0 avec.

[Archytas]

Salut, comment ?

[Ben314]

Par exemple, il écrit textuellement que, partant de -A=-1+1-1+1...
On "déduit" que 1-A=1-1+1-1+1... (ajout d'un terme et décalage d'un cran vers la droite)

De même, partant de X=1+1+1+1+1...
On "déduit" que 1+X=1+1+1+1+1...
C'est à dire 1+X=X et donc 1=0.

[Pseuda]

Dans le même genre (ou presque), on peut montrer que =2.

[Archytas]

D'accord merci ^^ !

[Doraki]

Pour compléter ce que dit Ben, voilà la "preuve" que 1+1+1+1+... existe (et vaut 0 ?) :

1+2+3+4+... = C
on décale
0+1+2+3+... = C
on soustrait terme à terme
1+1+1+1+... = 0

et avec ça tu obtiens bien 1=0.

[Archytas]

Ouais donc c'est bien la preuve que les notations qu'on emploie i.e. A = 1 - 1 + 1 - 1 +... sont juste des notations et que ça ne représente pas la "somme" de 1 et de -1 bête et méchante telle qu'on la connait puisqu'elle n'est pas définie ici et c'est comme ça qu'il semble l'employer...

[bolza]

On peut bien définir la suite Un par : U0 = 1 et U_n+1 = U_n + (-1)^(n+1).
où le "+" est "la" somme bête et gentille que l'on connaît.

Une manière propre d'exprimer la somme A est de dire que A est la limite de la suite Un
quand n tend vers l'infini. Le problème c'est que cette limite n'existe pas.
(ou du moins pas dans R en tout cas)

Cependant les mathématiques sont toujours pleines de surprises :
Un nombre réel par exemple est un nombre qui a un nombre fini de chiffre (non nuls) avant la virgule, et un
nombre infini de chiffres après la virgule.

Et si on s'intéressait aux nombres qui ont un nombre infini de chiffre avant la virgule, et un nombre
fini de chiffres (non nuls) après la virgule.

Par exemple considérons le nombre : .....9999999 (avec une infinité de 9 vers la gauche.
ajoutons 1 à ce nombre on a ......999999+1=.....00000=0 (car la retenu se propage à l'infini).
autrement dit : ....99999= -1 <-> .....11111= -1/9
ce qui peut s'écrire aussi : 1 + 10 + 100 + 1000 + .... = -1/9 (où le "+" est le "+" bête et gentil que l'on connaît).

Ce que je vous raconte ci-dessus est correct, sauf qu'on est plus dans le monde des réels que l'on connaît,
mais dans celui des nombres p-adiques (enfin presque, car ici l'exemple que j'ai donné est en base 10 et 10 n'est pas premier, mais l'idée est là).

Et il se trouve que la topologie des nombres p-adiques est complètement différente de la topologie sur R.
Et donc la notion de "convergence" (qui dépend de la topologie choisi) n'a plus du tout le même sens.
Donc dans l'exemple que j'ai donner, ce n'est pas tellement l'opération d'addition qui est en cause mais
la notion de convergence qui change.
(En fait R est une façon de compléter le corps des rationnels Q, et les nombre p-adiques en est une autre,
j'ai lu ça ici : https://fr.wikipedia.org/wiki/Nombre_p-adique)

Après ma culture s'arrête là, je n'ai jamais étudié la théorie des nombres p-adique et je n'ai absolument
aucune idée si cela a un lien avec le résultat 1+2+3+...=-1/12.

[Archytas]

Je pense que le problème de la vidéo vient plus du fait que le gars manipule des objets tels que le '+' veut manifestement dire autre chose dans ses notations que celui qu'on utilise usuellement avec les réels, complexes etc (comme par exemple le '+' des séries telles qu'on les définit par la convergence des sommes partielles (qu'on désigne principalement par le symbole sigma), mais on montre que le '+' des séries se comporte pas mal avec le '+' qu'on connait : on peut sommer deux série convergentes, on définir la somme d'un réel avec une série etc...) sauf que là il utilise le '+' qu'on connait avec le '+' de ses séries qui veut plus dire la même chose puisque A = 1 - 1 + 1 - ... devient plus qu'une bête notation A qui vaut 1/2 ? D'ailleurs l'incohérence qu'a montré Doraki soulève bien le fait qu'on peut pas faire n'importe quoi avec ces objets !
Arrêtez moi si je me trompe où que je dis des conneries, ça m'arrive souvent mais c'est comme ça que je l'ai compris