Bonjour les matheux,
J'ai considère une courbe continue, par exemple exprimée en polaire : Rho(theta)
Rho conserve un signe constant. La courbe est par exemple concave.
Je cherche à démontrer qu'un rayon de courbure de cette courbe qui est décroissant en fonction de theta implique une décroissance de Rho(Thêta). Rc' <0 ==> Rho' < 0
Je rencontre des difficultés : J'ai dérivé l'expression du Rc par rapport à thêta pour voir si j'arrivais à déduire qq chose de Rc'<0. Sans succès.
Est-ce que je cherche à prouver est vrai ? pour la spirale c'est OK, avez vous un contre exemple ?
Est-ce que je cherche à prouver est démontrable ?
Si oui, est ce déjà formulé sous forme d'un théorème?
Si c'est faisable mais non formulé, l'un d'entre vous pourrait il me suggérer les éléments pour le démontrer ?
Par avance merci.
Math-ieu
Variation du rayon de courbure et variation du rayon
2 messages
- Page 1 sur 1
Salut,
Normalement, le rayon de courbure d'une courbe, c'est le rayon du cercle qui approxime le mieux la courbe au voisinage d'un point donné (approximation à l'ordre 2)
Il y a des tas de façons de le calculer en fonction de ce que l'on connait de la courbe (équation cartésiennes ou paramétriques ou polaires ou... autre...)
Dans ton cas où tu as une équation polaire de la forme) , le rayon de courbure au point correspondant à un
, le rayon de courbure au point correspondant à un  donné est :
donné est : ^{\frac{3}{2}}}{\rho^2+2 \rho' ^2-\rho\rho''}\) (c.f. lien su wiki çi dessus)
(c.f. lien su wiki çi dessus)
Aprés, il n'y a plus qu'à se taper le calcul (un peu bourrin...) de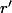 pour voir si effectivement
pour voir si effectivement 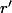 a le même signe que
a le même signe que 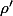 .
.
Normalement, le rayon de courbure d'une courbe, c'est le rayon du cercle qui approxime le mieux la courbe au voisinage d'un point donné (approximation à l'ordre 2)
Il y a des tas de façons de le calculer en fonction de ce que l'on connait de la courbe (équation cartésiennes ou paramétriques ou polaires ou... autre...)
Dans ton cas où tu as une équation polaire de la forme
Aprés, il n'y a plus qu'à se taper le calcul (un peu bourrin...) de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
