La série de Riemann pour des valeurs paires
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Anonyme
 par Anonyme » 07 Fév 2009, 20:02
par Anonyme » 07 Fév 2009, 20:02
La série de Riemman est définie par

Or

Pour toutes les valeurs de alpha paires, on retrouve un résultat du type Pi exposant k, multiplié par un rationnel (1/6, 1/90, 1/945...)
Comment détermine-t-on ce rationnel en fonction de k svp ? :help:
(les images sont de wikipédia)
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 07 Fév 2009, 20:05
par XENSECP » 07 Fév 2009, 20:05
Ce serait marrant de trouver une formule générale tient ... :D
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 07 Fév 2009, 20:09
par Monsieur23 » 07 Fév 2009, 20:09
Aloha ;
On peut utiliser les séries de Fourier pour démontrer ces résultats.
« Je ne suis pas un numéro, je suis un homme libre ! »
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 07 Fév 2009, 20:12
par XENSECP » 07 Fév 2009, 20:12
Monsieur23 a écrit:Aloha ;
On peut utiliser les séries de Fourier pour démontrer ces résultats.
Certes mais de là à trouver le coefficient comme ça

-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 07 Fév 2009, 20:14
par Monsieur23 » 07 Fév 2009, 20:14
J'sais pas, j'ai jamais vraiment aimé les séries de Fourier ! :lol5:
Par contre, il me semble que j'avais fait un DS en sup qui démontrait ça dans le cas général.
J'vais chercher, mais c'est pas gagné que je le retrouve ! :lol5:
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 07 Fév 2009, 20:32
par Monsieur23 » 07 Fév 2009, 20:32
C'est bien ça.
On définit une suite de polynômes (Bn) vérifiant :
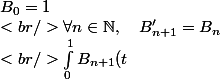 dt = 0 \\)
On montre ensuite que
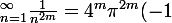^{m-1} B_{2m}(0)\times \frac12)
Voilà voilà !
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 07 Fév 2009, 22:07
par Doraki » 07 Fév 2009, 22:07
Le moyen le plus facile pour calculer ça c'est de démontrer et d'utiliser la formule
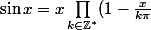 = x - x^3/3! + x^5/5! - ...)
développer le produit et identifier les coefficients donne ce qu'il faut.
-
Anonyme
 par Anonyme » 08 Fév 2009, 12:08
par Anonyme » 08 Fév 2009, 12:08
Désolé mais je n'ai pas compris, quelle est donc cette formule ? Vous en avez donné 2 différentes... :(
Bn c'est la suite de la fonction exponentielle ? Désolé pour ces questions je ne suis qu'en terminale..
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités



