Le saviez-vous ? (arithmétique)
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 23 Déc 2007, 00:09
par Flodelarab » 23 Déc 2007, 00:09
Salut :salut:
^2=\(\sum_{i=1}^n i^3\) \qquad ,\forall n \in \mathbb{N}^*) Le saviez vous ?
Le saviez vous ?Exemple:
(1 + 2 + 3 + 4 )² = 10² = 100 = 1 + 8 + 27 + 64 = 1³ + 2³ + 3³ + 4³
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 23 Déc 2007, 00:13
par Nightmare » 23 Déc 2007, 00:13
Oui :lol3: :lol2:
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 23 Déc 2007, 00:29
par _-Gaara-_ » 23 Déc 2007, 00:29
lol oui ^^ on le démontre par récurrence

c'est sympa comme démonstration même


-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 23 Déc 2007, 09:39
par lapras » 23 Déc 2007, 09:39
je ne savais pas !
C'est jolie ! :happy2: (par contre la démonstration par récurrence n'est pas tres interessante)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 23 Déc 2007, 09:42
par leon1789 » 23 Déc 2007, 09:42
Plus intéressant est de retrouver les formules de sommation (en tout degré 1,2,3,4,...), non ? :happy2:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 23 Déc 2007, 09:46
par ThSQ » 23 Déc 2007, 09:46
Oui :we:
Y'a plein de preuves, dont une géométrique très zoulie.
Et cela invite naturellement à l'exo (de mon invention :girl2: ) :
Quelles sont les suites (de nombres réels positifs (facile) et quelconques (:spy:)) telles que
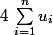^2=\(\sum_{i=1}^n {u_i}^3\) \qquad ,\forall n \in \mathbb{N}^*)
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 23 Déc 2007, 09:59
par lapras » 23 Déc 2007, 09:59
Je propose de faire une "récurrence"
tu prend U0 tel que ca soit vrai
tu veux que ca soit vraie pour le suivant :
ca équivaut à dire que 2*Somme(Ui)*U_(i+1) + U_(i+1)² = U_(i+1)^3
U_(i+1)² - U_(i+1) - 2*Somme(Ui) = 0
c'est un polynome du second degré en U_(i+1)
on prend donc U_(i+1) = (1 + sqrt(1+8*Somme(Ui))/2
Donc la condition de départ c'est U0² = U0^3
soit U0²(U0 - 1) = 0
soit U0 = 0 ou U0 = 1
la seule suite possible reste donc celle de flodelarab
-
SimonB
 par SimonB » 23 Déc 2007, 16:29
par SimonB » 23 Déc 2007, 16:29
ThSQ a écrit:Y'a plein de preuves, dont une géométrique très zoulie.
J'aime beaucoup, c'est au départ une des nombreuses "preuves sans mots" des mathématiciens chinois, dont la simplicité et la beauté sont à admirer.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 24 Déc 2007, 17:36
par ThSQ » 24 Déc 2007, 17:36
Bon c'était très facile le cas positif. Le cas général maintenant !
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 24 Déc 2007, 18:21
par lapras » 24 Déc 2007, 18:21
On peut prendre la solution négative de mon trinome

-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 24 Déc 2007, 20:19
par ThSQ » 24 Déc 2007, 20:19
Tsss .
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 25 Déc 2007, 17:34
par Flodelarab » 25 Déc 2007, 17:34
lapras a écrit:On peut prendre la solution négative de mon trinome

Ben en fait, oui. Je ne comprends pas pourquoi tu as éliminé d'office cette partie de ta première démo.
Car il y a bien 3 suites qui fonctionnent (sur les 4 possibles) et non 2:
* La suite des entiers consécutifs (partant de 0 ou de 1)
* La suite de zéros
Le 4ème cas donnant 0;1;-1 est impossible puisqu'on a dit "positifs".
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 25 Déc 2007, 17:57
par _-Gaara-_ » 25 Déc 2007, 17:57
ThSQ a écrit:Tsss .
:doh: :hein: huh ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité