On connaît assez souvent les fonctions homographiques. Ce sont les fonctions de la forme
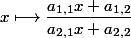
avec
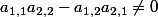
.
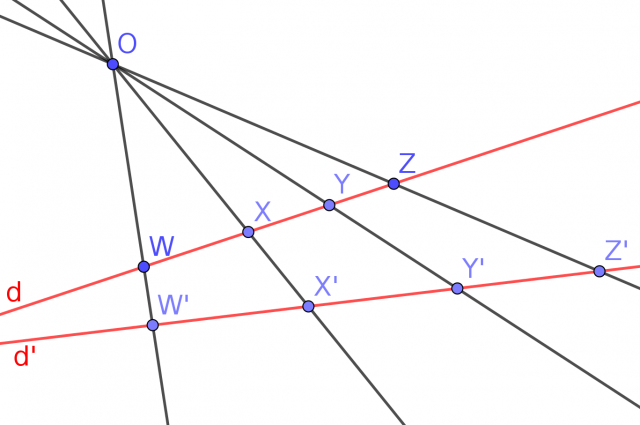
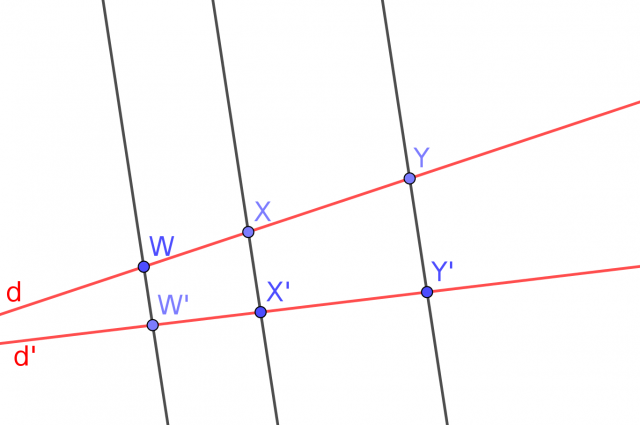
Elles peuvent s'étendre à la droite projective obtenue en ajoutant un point

à l'infini à la droite. Étant donné deux triplets
)
et
)
de points distincts sur la droite, il existe une et une seule fonction homographique qui envoie le premier triplet sur le deuxième. En particulier, l'unique fonction homographique qui envoie le triplet
)
sur le triplet
)
est
/(c-a)}{(x-b)/(c-b)}\;.)
On peut remarque que l'image de

par cette fonction homographique est justement le birapport
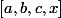
.
Passons maintenant de la droite au plan. Une homographie du plan est une transformation de la forme
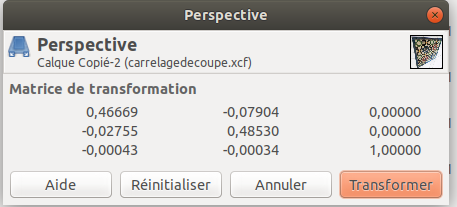
 \longmapsto \left(\dfrac{a_{1,1}x+a_{1,2}y+a_{1,3}}{a_{3,1}x+a_{3,2}y+a_{3,3}}, \dfrac{a_{2,1}x+a_{2,2}y+a_{2,3}}{a_{3,1}x+a_{3,2}y+a_{3,3}}\right)\;,)
où le déterminant de la matrice
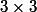
de coefficients
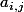
est non nul. Une telle homographie s'étend au plan projectif obtenu en ajoutant un point à l'infini pour chaque direction de droite. Une homographie est donc donnée par les neuf coefficients
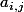
, à un facteur scalaire près (multiplier tous les
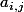
par un même

donne la même homographie). On a ainsi huit degrés de liberté.
Étant donné deux quadruplets
)
et
)
de points dans le plan (tels que trois points d'un quadruplet ne soient jamais alignés), il existe une unique homographie du plan qui envoie le premier quadruplet sur le deuxième. On retrouve bien les huit degrés de liberté puisque chaque point du plan est repéré par deux coordonnées.
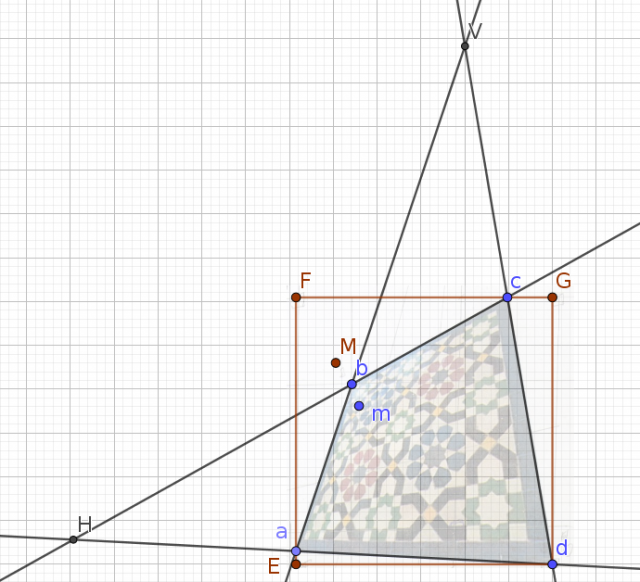
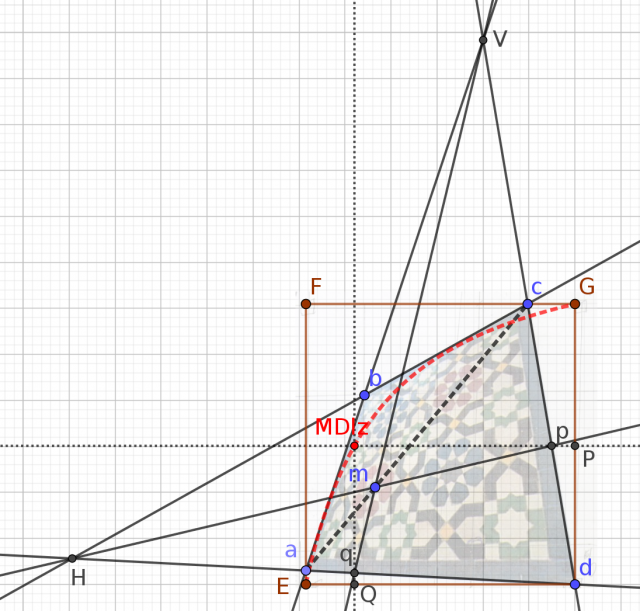
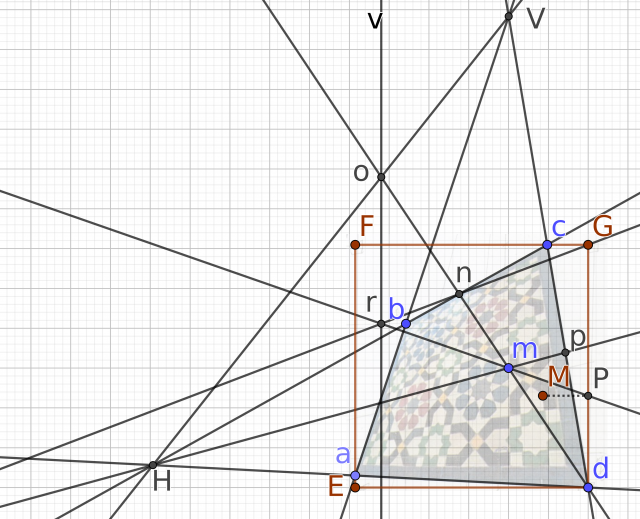
Le redressement que l'on cherche, c'est l'unique homographie qui envoie le quadruplet
)
(les coins du carrelage) sur le quadruplet
)
(les coins du rectangle). On cherche les neuf coefficients de l'homographie, en fait huit puisque l'on peut en fixer un arbitrairement vu la proportionalité. Une personne qui n'y connaît rien peut trouver que neuf ou huit, ça fait beaucoup. Nous avons vu que c'est en fait dans la nature des choses : on a huit degrés de liberté pour définir une homographie, de même qu'on a six degrés de liberté pour définir une transformation affine du plan, et trois degrés de liberté pour définir un déplacement du plan.
Dans notre problème de redressement, on a en fait le point

qui est fixe et que l'on peut prendre comme origine du repère. Ça simplifie l'écriture de l'homographie de redressement cherchée, qui est alors de la forme
 \longmapsto \left(\dfrac{a_{1,1}x+a_{1,2}y}{a_{3,1}x+a_{3,2}y+1}, \dfrac{a_{2,1}x+a_{2,2}y}{a_{3,1}x+a_{3,2}y+1}\right)\;,)
avec
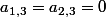
et
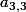
que l'on peut prendre égal à

. On n'a donc plus que six coefficients à déterminer. Suite au prochain numéro.