beagle a écrit:ce truc est un peu le dada de Pierre qui ne peut communiquer sur ce forum.
Pourquoi (si cela n'est pas indiscret) ?
beagle a écrit:ce truc est un peu le dada de Pierre qui ne peut communiquer sur ce forum.
leon1789 a écrit:Bonsoir
L.A. , vous dites bien que vous travaillez dans l'espace 3D pour transformer cette figure du plan ? j'ai peut-être mal compris.

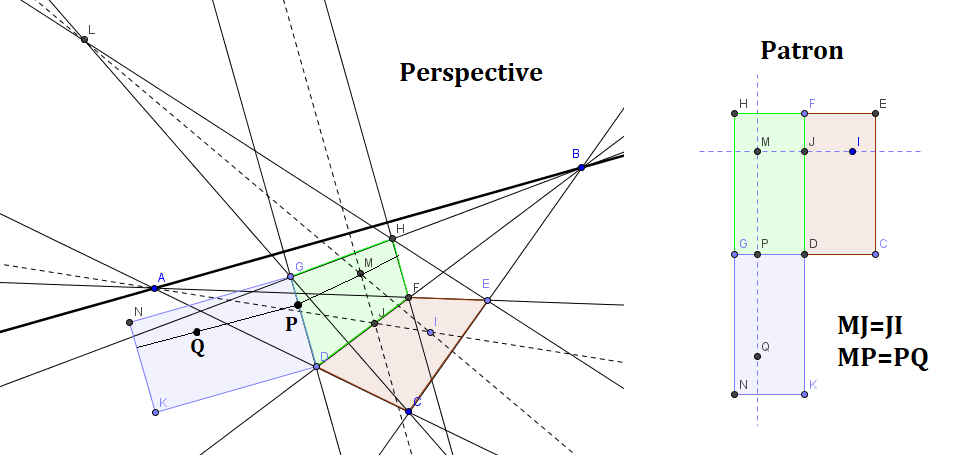
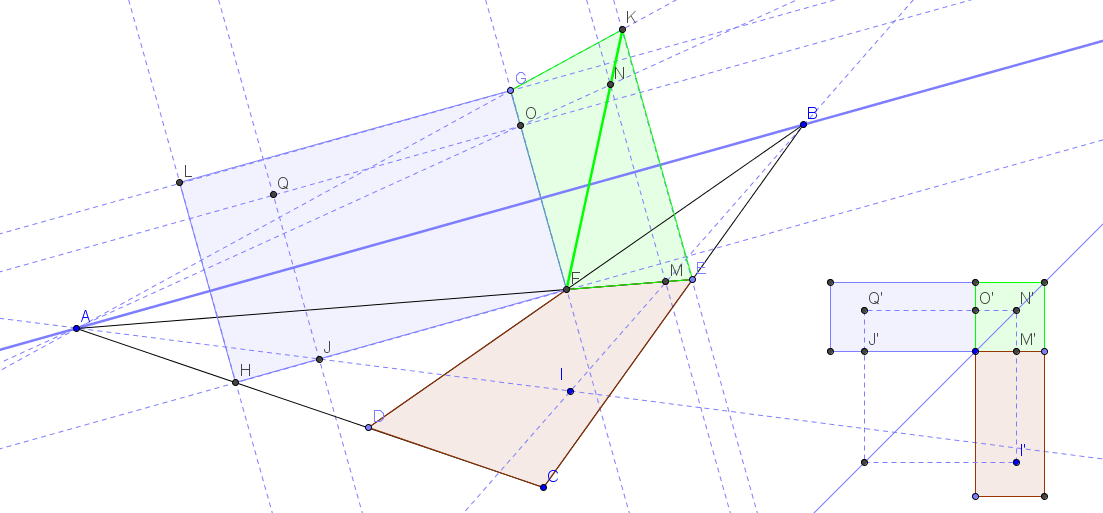
Merci pour votre réponse sur cette question.L.A. a écrit:Qui dit perspective dit projection d'un espace 3D sur un espace 2D. La construction se fait entièrement dans l'espace 2D final, mais peut prendre appui sur un espace 3D initial qui donnerait lieu à cette projection. Ici, dans mon espace 3D, les trois quadrilatères rouges, vert et bleu sont trois rectangles de mêmes dimensions, le premier horizontal et les autres verticaux, qui se touchent par une arête, comme un patron.
leon1789 a écrit:L.A. a écrit:Mais vous n'avez pas répondu par rapport aux calculs : avec "les mains dans le moteur" (regardons la réalité des calculs), quand on calcule les coordonnées des nouveaux points, ces calculs se font-ils avec des expressions polynomiales de degré 1, 2, 3,... ? avec quelques divisions ou sans aucune division ?

Idriss a écrit:beagle a écrit:ce truc est un peu le dada de Pierre qui ne peut communiquer sur ce forum.
Pourquoi (si cela n'est pas indiscret) ?
beagle a écrit:LA solution ne parle pas de la solution de LA , mais bien du dictatorial LA UNIQUE SEULE ...
beagle a écrit:Pour ne prendre que l'exemple de ce fil de discussion,
la méthode de LA, comme le logiciel de Pierre répondent-ils correctement à un problème, oui, non?
est indépendant de on peut le faire autrement , mieux formulé , plus généralisable etc...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :