Recherche de courbes avec limite

[ronandroid]

Bonjour a tous,

Actuellement en train de développer un jeu (sur le genre pokemon... si ça intéresse certains fureter sur myphonster pour plus de détails)
je cherche à donner accès à mes joueurs à une quantité évolutive (je ne vois pas comment le dire autrement) de créatures selon leur niveau.

En l’état, j'ai 66 créatures, j'aimerai donc qu'une fois arrivé à un niveau Z, ils aient accès à toutes ces créatures, et qu'au niveau Z+n, ce nombre n'augmente pas. Je recherche donc une courbe sur la forme logarithme népérien, j'ai actuellement trouvé ça de plus approchant : 10*ln((x)/8)+39

seulement, je ne sais pas comment :
1/ définir mon maximum (dans cette formule, on ne trouve nulle part mon "66")
2/ définir le niveau à partir duquel on atteint ce maximum
3/ réduire un peu la "vitesse" de montée de la courbe

Pour le point 3, j'ai cherché sur cette courbe : 1.7*sqr(x*20)+4 (sqr = racine carré)
Pour le point 1, je m’étais orienté sur : 66*sin(x*pi/200)
(pour le point 2 en revanche, je ne sais pas comment y arriver)

Mon problème, c'est que je ne peux pas me servir de mes fonctions :
- racine carré, car elle n'a pas de limite
- sinusoïdale car trop faible en montée (je ne peux pas frustrer mes utilisateurs...) et on n'atteint pas assez vite ma limite, et une fois le lvl 100 passé... ça redescend, c'est dommage, donc je m’étais ensuite orienté sur 39*atan(x)... mais là encore, a moins de "test" hasardeux, impossible de définir d'une limite (et la montée est bien trop prononcée au début)

Pour résumer, je rechercherai une fonction avec le début de ma courbe de racine carré, le milieu (là ou elle croise) de ma lognep et la fin de ma sinusoïdale... ou approchant, les valeurs ne sont pas "figées" j'aimerai juste obtenir la meme tendance, avec de la simplicité pour rentrer mes valeurs limites


Par avance merci d'avoir lu ce message et pour toutes aides apportées

[fatal_error]

slt,

peux-tu joindre une courbe (tracee a la main par exemple) qui illustre ce que tu aimerais avoir?

[Ben314]

Salut,
De ce que je comprend de ton problème, tu voudrait une courbe qui "monte" et qui, au bout d'un certain temps se "stabilise" à la valeur 66 (nombre max de monstres).
Perso, le premier truc qui me vient à l'esprit, c'est où E(?) désigne la partie entière, un réel de 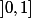et a et b des réels positifs.
Ces 3 réels sont à déterminer en fonction du nombre de monstres que tu veut avoir au niveau 0 (ou 1), de la vitesse à laquelle tu veut que ça monte et du niveau à partir duquel tu veut que le nombre de monstre soit stabilisé à 66.
Si la "vitesse de croissance" ne te va pas, tu peut remplacer la division par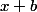 par une division par ou ou... n'importe quoi qui tend vers l'infini quand x tend vers l'infini.

P.S. Si ton 39atan(x) "monte trop vite" au début, remplace le par un 39atan(x/2) ou plus généralement un 39atan(ax+b) où tu choisi a et b... comme tu veut...

P.S.2 : vu que tu ne semble pas aller jusqu'à des niveaux "archi hyper élevés", pourquoi ne fait tu pas "à la main" un petit tableau informatique niveau->nombre de monstre qui va par exemple du niveau 1 au niveau 80 et en considérant qu'à partir du niveau 80, tu as automatiquement 66 monstres.

[ronandroid]

@fatal_error, etant sur smartphone, c'est pas la joie pour joindre un document fait main, je me base sur http://grapheur.cours-de-math.eu/
Merci Ben314, ça c'est de la rapide rapide et détaillée.
Néanmoins j'ai quelques questions/précisions :
- pour la forme entière, un (int) suffira
- pour le "e bizarre" (que j'arrive pas a reproduire...) s'il est égale a 0 ou 1, a quoi sert il... c'est pour le "niveau" de démarrage ?
- a et b, aurais tu des "valeurs" ou un "rapport" entre les 2 (genre a>b ou 2a=b, etc...) histoire que je vois ce que ça donne...

car pour l'heure, parti sur un 66+1-550/(x+8) ça rend pas trop mal (bien que je n'arrive pas a mes 66....)

pour ton PS : je ne vois pas comment "définir" mon "66"
Pour ton PS2: j'y avais bien pensé, mais l’inconvénient de cette méthode est quelle est "statique" et comme mon nombre de phonsters (les créatures) va évoluer (je ne sais pas encore à quel rythme)... ça risque d’être contraignant
(qui plus est, je ne sais pas encore comment va "évoluer" le joueur, je pensais a quelques chose du genre 1.25*niveau^3 ... donc une évolution "lente" vers les haut niveaux, comme les bas niveaux) d'où le fait que je recherche une formule...

[ronandroid]

La plus belle que j'ai trouvé c'est 66-(100/(x/15+1.5))+1
Mais... ca n'arrive a 66 qu'a partir de ......pfiou.....sacrément loin

[Ben314]

a) Désolé pour le retard sur les réponses : je suis en vacance dans un coin sans wifi donc je me connecte.... quand je peut...

- pour la forme entière, un (int) suffira
- pour le "e bizarre" (que j'arrive pas a reproduire...) s'il est égale a 0 ou 1, a quoi sert il... c'est pour le "niveau" de démarrage ?
- a et b, aurais tu des "valeurs" ou un "rapport" entre les 2 (genre a>b ou 2a=b, etc...) histoire que je vois ce que ça donne...
car pour l'heure, parti sur un 66+1-550/(x+8) ça rend pas trop mal (bien que je n'arrive pas a mes 66....)

Les deux premières questions sont liées (le (int) et le "epsilon" ) : ton "nombre de monstres", ça doit être un entier (je suppose...) alors que la plupart des formules de math. qu'on peut essayer donnent des réels qu'il faut ensuite transformer en entier. En math, "LA" fonction dédiée à ça, c'est la "partie entière" E(x) qui te renvoie le plus grand entier inférieur à x. Par exemple E(2.35)=2; E(3.983)=3. Le transtypage (int) en info permet aussi de convertir un réel en entier, et, il me semble (donc... à vérifier...) que le résultat renvoyé est l'entier le plus proche du réel de départ : (int)2.35 -> 2 mais (int) 3.983 -> 4.
Aprés, si tu considère par exemple le réel F=66-550/(x+8), lorsque x va être extrèmement grand, F va être un tout petit peu inférieur à 66 (du style F=65.983) et la partie entière (au sens mathématique) de F sera 65 et tu pourra continuer à augmenter x, ça restera "coincé" à 65 sans jamais atteindre 66.
Si tu veut que ça finisse par atteindre 66, il faut mettre un truc du style F=66.7-550/(x+8) : quand x sera "immense", F vaudra un tout petit peu moins de 66.7 et la parti entière sera bien 66.
Visiblement, tu t'es rendu compte tout seul du problème en mettant directement F=66+1-550/(x+8) qui, lorsque x est trés grand, vaut un tout petit peu moins de 67 donc la partie entière sera 66 (mais j'aurais pensé que le (int) allait te donner 67 pour x trés trés grand...)
Si tu veut atteindre plus vite la barre "fatidique" des 66 monstres, tu peut tout à fait mettre un +1.5 voire même un +2.1 ou +2.5 à la place du +1, mais il faudra faire un test vu que dans ce cas, pour x trés trés grand, ça risque de passer à 67 monstres, voire 68.
Concernant le a et le b et le fameux epsilon, je n'ai aucun "à priori" sur qui doit être grand par rapport à qui...
A mon avis, il faut commencer par regarder de façon générale ce que ça va donner au niveau 1 (ou 0, je sais pas ou tu commence) et à quel niveau ça va faire 66. C'est un calcul trés simple, mais il faudrait savoir comment marche le (int) sur ta machine : est ce que le (int) de 3.98 renvoie 3 ou 4 ?

[Ben314]

La plus belle que j'ai trouvé c'est 66-(100/(x/15+1.5))+1
Mais... ca n'arrive a 66 qu'a partir de ......pfiou.....sacrément loin

Au lieu du "+1" final, essaye "+1.5" ou bien "+2" et rajoute un test derrière pour que, si le résultat dépasse strictement 66, ça le ramène à 66.

[ronandroid]

le but surtout c'etait que ce soit "la formule" qui se gère de "bloquer"
ensuite c'est surtout que, lvl 30/40 j'aimerai assez qu'il ait accés aux 66 monstres ...
Seul souci, lorsque j'aurai plus de monstres, il faudrait pas que ce soit ce lvl 40, mais , de facon "logique" en suivant la courbe, ca arrive genre lvl 50 pour 70/75 monstres
Au final, je pense que je vais prendre la formule de racine carré et la "limiter" moi meme... ca sera le plus "simple" pour faire ce que j'avais dans l'esprit
mais merci quand meme pour ton aide et tes idées, je m'y repencherai peut etre ulterieument quand j'arriverai mieux a exprimer mon besoin :)