Problème sur une suite

[JimBvrd]

Bonjour à tous, j'ai déjà posé cette question dans la rubrique études supérieures mais vu que c'est pas du soutient scolaire, personne ne m'a répondu.

J'ai en fait fait une erreur de raisonnement dans mon problème qui est le suivant :
Imaginons un parieur qui a un capital de départ de 250€ et qui mise 6% de son capital (il réinvestit à chaque fois) sur une côte fixe à 1.8
On a donc ici une suite...
Au bout de combien de temps dégagera-t-il un bénéfice de 1000€ par pari ?
Avec Excel je trouve (veuillez me pardonner, je n'ai pas déterminé la raison ni rien, la récurrence et moi ne sommes pas très bon amis) :
au bout de 96 paris.

Le parieur se fixe comme objectif d'y arriver en 1 an maximum ; trouver son taux de réussite minimum ?
On a donc le système suivant (X représente les paris gagnés et Y les paris perdus):
X+Y = 365
X = Y + 96
Après avoir résolu le système on se rend compte qu'il a donc besoin d'un taux de réussite de 63% minimum.

Seulement voilà, dans mon calcul je pense que je n'ai pas pris en compte le fait que lorsqu'il y a défaite, les 6% misés au coup d'après deviennent plus faibles, étant donné qu'on perd une mise entière. Par quel moyen corriger cette erreur ?

Merci d'avance pour vos précieuses aides !

[Ben314]

Salut,
Bon, déjà, une réponse propre à la question 1 :
Si désigne la somme qu'il a juste avant le n ième pari alors 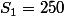et, lors du n-ièma paris, il mise et, s'il gagne, il empoche (si j'ai bien compris ce qu'est une "cote"...) soit un bénéfice de .
On aura donc .
À chaque pari sa cagnote est multiplié par donc aprés paris elle est multiplié par 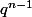et donc .
Le bénéfice lors du n-ième pari est donc de et il sera à condition que c'est à dire , c'est à dire .

Pour la question 2), appelons le nombre de paris réussis et 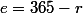le nombre d'échecs dans l'année.
On vient de voir qu'à chaque réussite, sa cagnote est multipliée par .
Lors d'un échec, sa cagnote est multipliée par
Juste avant le dernier pari qu'on suppose réussi, donc aprés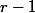 réussites et 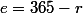échecs sa cagnote a été multiplié par ... et comme au départ elle valait 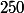euros, elle est égale à ...
Lors du dernier pari (réussi) de l'année, il fera un bénéfice de ... qui sera >1000 à condition que ...

[JimBvrd]

Bonjour, merci beaucoup pour votre réponse !
Je me suis très mal exprimé en fait car j'ai mélangé l'énoncé avec mes propres calculs qui sont faux ! (du moins c'est pas ce que j'attendais dans la partie 2)

Voici l'énoncé :
Imaginons un parieur qui a un capital de départ de 250€. Il mise tout le temps 6% du capital sur une côte fixe à 1.8, une fois par jour. Donc, en cas de gain, il récupère sa mise majorée de 80% et en cas de perte, il perd la totalité de sa mise.
1) S'il a un taux de réussite de 63%, au bout de combien de jours pourra-t-il arriver à un mise de 1250€ ?
2) S'il veut arriver à une mise de 1250€ en 365 jours, quel devra être son taux de réussite ?

La suite est mise en place et c'est déjà un bon point de départ mais le plus dur reste d'y introduire le cas où l'échec est envisageable.
En cas d'échec (j'ai toujours pas progressé en math depuis 10 minutes ^^) il perdrait donc à chaque fois 6,38% de son capital (merci Excel) ce qui est donc q'.
Je me trompe peut être ?

Mais après, comment mettre en relation la probabilité de réussite, le temps, et la suite ?

[Ben314]

S'il échoue, il perd sa vise donc : .

Vu qu'on te demande pas des proba comme résultat mais des valeurs "fixes", la seule façon de faire les calculs, c'est de supposer que, lors de paris, il y a en a exectement de réussi et de ratés.
Tu en déduit que, durant ce laps de temps, sa cagnote est multiplié par

[JimBvrd]

J'ai RIEN compris...
q' = 47/50 (faute de frappe ? ou alors je suis encore plus perdu que c'que je pensais)
La cagnotte est donc multipliée par q^r x q'^e = 0.66% ? Ce n'est pas possible, c'est trop peu comme valeur
Pour le 1) je pensais qu'il fallait faire 0.63U(n) - 0.37V(n) = 1250 et résoudre l'équation (où U(n) représente la suite des succès et V(n) la suite des échecs)
Pour le 2) je pensais qu'il fallait faire XU(365) - (1-X)V(365) =1250 et résoudre l'équation de la même manière.

[Ben314]

Oui, q'=47/50.
Aprés, à chaque réussite, la cagnote est multiplié par et, à chaque echec, elle est multiplié par .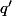
Aprés réussite elle est multipliée par (c'est la définition d'une puissance...) et aprés echecs elle est multipliée par .
L'ordre des réussite/echecs n'a pas d'importance vu que dans un calcul du style l'ordre dans lequel sont les et les 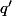n'a pas d'importance.

avec soit effectivement un gain (moyen) d'environ 0.67% de la cagnote à chaque pari.
C'est peu, mais il faut bien voir que déjà, il ne mise que 6% de la cagnote, que la cote n'est pas immense et qu'en plus il risque de perdre : c'est déjà pas mal que ce soit positif en terme de pourcentage (i.e. que ) : s'il gagnait un peu moins souvent que 63% des cas, il aurait une espérance de gain négative (i.e. )

[JimBvrd]

C'est trop bizarre. Mathématiquement ce que vous dites est juste, mais imaginons un taux de réussite de 60% on aurait au 6 paris réussis, puis 4 échoués (peut importe l'ordre vous avez dit)
Donc 6 paris réussis : 331.21
moins les 4 paris échoués : 331.21*0.94^4 =258.6
L'évolution est donc de 3.3%

Et là après avoir écrit je me rends compte qu'on a parlé de l'évolution par pari et non évolution générale, lol. (faute d'inattention, toute ma scolarité)
Mais donc on a pas du tout répondu au 1) et 2), on fait comment pour ces questions ?

Clairement on a dit exprimé Sn+1 mais que vaut Sn par rapport à S0 en cas d'échec ?

Désolé d'insister et d'abuser de votre patience, j'ai l'impression d'être un âne à ne pas comprendre ça.

[Ben314]

Pour un taux de réussite de 60%, ça ferait (même calculs, seul l'application numérique change) :
: environ 0.34% de gain. (c'est encore positif...)
Par contre, avec un taux de réussite de 55%, on trouve
: donc environ 0.2% de perte.

Aprés, concernant le 1), on vient de voir qu'à l'issue de paris, la cagnote est (en moyenne) multipliée par 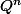(où ), donc juste avant le -ième pari il peut espérer (en moyenne) avoir Euros ce qui signifie qu'au -ième pari il mise et il n'y a plus qu'à résoudre (en passant au logarithmes)

[Ben314]

Pour la question 2, tu note le fameux "taux de réussite" cherché.
Sur jours il y aura donc (en moyenne) réussites et échecs.
La cagnote aura donc été multipliée par et sera égale à
Donc la mise le 365-em jour sera de