Bonsoir!
Alors voilà, en revoyant le chapitre des Expressions Algébriques, et en révisant un peu les identités remarquables (programme de troisième, quoi), j'ai eu l'idée de commencer d'essayer de factoriser des polynômes du second degré avec la méthode du discriminant. Je m'en sors pas mal, après tout ce n'est qu'une application simple de formules connues, et trouvées..!
Je me demande s'il est possible pour moi d'apprendre à factoriser des polynômes plus 'gros' (troisième ou quatrième degré), quoique sachant qu'il faut un niveau élevé pour le faire.
Ces méthodes sont-elles accessibles pour moi, même difficilement?
Sinon, je laisse tomber!
Merci pour votre aide! :happy3:
Polynôme du troisième degré..!
6 messages
- Page 1 sur 1
Polynôme du troisième degré..!
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
C'est juste un peu (beaucoup) plus compliqué que pour le degré 2.
Et t'es obligé d'utiliser les nombres complexes (qui ont été introduits pour justement résoudre ce problème)
On cherche les racines x,y,z alors qu'on connaît a = x+y+z, b = xy+yz+zx, et c = xyz.
En notant j une racine cubique complexe de 1, on peut faire comme ça :
- on calcule ((x+jy+j²z)^3 - (x+j²y+jz)^3)² en fonction de a b et c (c'est le discriminant du polynôme)
- on en prend une racine carrée pour obtenir (x+jy+j²z)^3 - (x+j²y+jz)^3
- on calcule (x+jy+j²z)^3 + (x+j²y+jz)^3 en fonction de a b et c.
- on combine les deux trucs pour obtenir (x+jy+j²z)^3.
- on en prend une racine cubique pour obtenir (x+jy+j²z).
- on calcule (x+jy+j²z) * (x+j²y+jz) en fonction de a b et c.
- on en déduit (x+j²y+jz).
- on combine (x+jy+j²z) et (x+j²y+jz) avec (x+y+z) pour obtenir x, y, et z.
Alors que le degré 2 se résume à
- on calcule (x-y)² en fonction de (x+y) et xy
- on en prend une racine carrée pour obtenir (x-y)
- on combine les deux pour obtenir x et y.
Et t'es obligé d'utiliser les nombres complexes (qui ont été introduits pour justement résoudre ce problème)
On cherche les racines x,y,z alors qu'on connaît a = x+y+z, b = xy+yz+zx, et c = xyz.
En notant j une racine cubique complexe de 1, on peut faire comme ça :
- on calcule ((x+jy+j²z)^3 - (x+j²y+jz)^3)² en fonction de a b et c (c'est le discriminant du polynôme)
- on en prend une racine carrée pour obtenir (x+jy+j²z)^3 - (x+j²y+jz)^3
- on calcule (x+jy+j²z)^3 + (x+j²y+jz)^3 en fonction de a b et c.
- on combine les deux trucs pour obtenir (x+jy+j²z)^3.
- on en prend une racine cubique pour obtenir (x+jy+j²z).
- on calcule (x+jy+j²z) * (x+j²y+jz) en fonction de a b et c.
- on en déduit (x+j²y+jz).
- on combine (x+jy+j²z) et (x+j²y+jz) avec (x+y+z) pour obtenir x, y, et z.
Alors que le degré 2 se résume à
- on calcule (x-y)² en fonction de (x+y) et xy
- on en prend une racine carrée pour obtenir (x-y)
- on combine les deux pour obtenir x et y.
Merci pour vos réponses.
En fait, à ce que je sache, il existe plusieurs méthodes pour travailler, non? J'en ai entendu parler.. Pourriez-vous me donner des pistes un peu plus accessibles, s'il vous plait ce serait sympa :)
En fait, à ce que je sache, il existe plusieurs méthodes pour travailler, non? J'en ai entendu parler.. Pourriez-vous me donner des pistes un peu plus accessibles, s'il vous plait ce serait sympa :)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Salut,
Si tu veut une méthode qui utilise (lorsque c'est possible) un peu moins les nombre complexes, partant de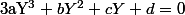 , tu divise par
, tu divise par  (évidement supposé non nul) puis tu dit que les deux premiers termes
(évidement supposé non nul) puis tu dit que les deux premiers termes 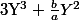 ) c'est le début du développement de
) c'est le début du développement de ^3) (jusque là, c'est un peu comme celles du second degrés).
(jusque là, c'est un peu comme celles du second degrés).
Tu pose alors (c'est à dire
(c'est à dire  ) et tu as une équation de la forme
) et tu as une équation de la forme 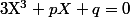 où
où  et
et 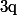 sont deux réels.
sont deux réels.
Ensuite, va voir le post #10 de cette discution
Aprés, la méthode de Cardan n'est quasi d'aucun intérêt "pratique" pour trouver les racines : mêmes si les racines sont trés simples (par exemple entières), tu ne le verra pas avec les méthodes de Cardan qui t'en donneront une expression trés compliquée. C'est à mon avis la raison pour laquelle cette méthode n'est enseigné qu'en Master comme une jolie application de la théorie de Galois.
Si tu veut une méthode qui utilise (lorsque c'est possible) un peu moins les nombre complexes, partant de
Tu pose alors
Ensuite, va voir le post #10 de cette discution
Aprés, la méthode de Cardan n'est quasi d'aucun intérêt "pratique" pour trouver les racines : mêmes si les racines sont trés simples (par exemple entières), tu ne le verra pas avec les méthodes de Cardan qui t'en donneront une expression trés compliquée. C'est à mon avis la raison pour laquelle cette méthode n'est enseigné qu'en Master comme une jolie application de la théorie de Galois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
