Perspective conique en programmation

par **Carat** » 28 Juil 2014, 17:12

Salut tout le monde,

Imaginons un plan de 500 x 500...
Imaginons un point (x, y, z):
- x = position sur la largeur
- y = position sur la hauteur
- z = position sur la profondeur
Imaginons que le centre de mon plan (250, 250) est le point de fuite de la perspective conique...

Quelle serait la formule a appliquer pour que mon point, en fonction de sa profondeur, se rapproche ou s'eloigne de ce point de fuite (pour simuler la profondeur en 2d)?

Merci :)

par **DamX** » 28 Juil 2014, 17:44

Bonjour,

La perspective conique avec le point de fuite au centre ce n'est jamais qu'une projection classique de type "camera", alors autant modéliser ça par une camera où le plan focal serait l'écran 500x500.

la camera est centre en (0,0,-f) avec f la focale. Pour trouver un point, il suffit de relier ce point avec le centre de la camera et de regarder l'intersection avec le plan focal en z=0, qui correspondra aux coordonnées que tu recherches.

donc si tu disposes d'un point (x,y,z), tu veux l'intersection entre la droite d'équation (250,250,-f)+t(x-250,y-250,z+f) et le plan z=0.

Ce qui donne donc -f+t(z+f)=0 => t=f/(z+f), et les coordonnées du point sur l'écran sont donc (250+t(x-250), 250+t(y-250)), à savoir (250+(x-250)f/(z+f),250+(y-250)f/(z+f)).

Une petite image trouvée sur le net illustrant le concept :

C'est tout simple. La chose amusante si tu programmes ça en te permettant de changer la valeur de la focale rapidement voire run-time c'est que tu te rends bien compte de son rôle : plus la focale est grande, moins la perspective est forte et le point de fuite visible, à la limite f infinie tu retrouves une perspective isométrique/cavalière (tu obtiens (x,y) en faisant tendre f vers l'infini). A l'opposé plus la focale est faible et plus tout semble rapidement "aspiré" vers le point de fuite (tu obtiens (250,250) en faisant tendre f vers 0).

Tu peux même ensuite t'amuser à déplacer le point de fuite en prenant (x0,y0,-f) comme centre de la caméra (sans rien changer au reste).

Damien

par **Carat** » 28 Juil 2014, 19:19

DamX a écrit:Bonjour,

La perspective conique avec le point de fuite au centre ce n'est jamais qu'une projection classique de type "camera", alors autant modéliser ça par une camera où le plan focal serait l'écran 500x500.

la camera est centre en (0,0,-f) avec f la focale. Pour trouver un point, il suffit de relier ce point avec le centre de la camera et de regarder l'intersection avec le plan focal en z=0, qui correspondra aux coordonnées que tu recherches.

donc si tu disposes d'un point (x,y,z), tu veux l'intersection entre la droite d'équation (250,250,-f)+t(x-250,y-250,z+f) et le plan z=0.

Ce qui donne donc -f+t(z+f)=0 => t=f/(z+f), et les coordonnées du point sur l'écran sont donc (250+t(x-250), 250+t(y-250)), à savoir (250+(x-250)f/(z+f),250+(y-250)f/(z+f)).

Une petite image trouvée sur le net illustrant le concept :

C'est tout simple. La chose amusante si tu programmes ça en te permettant de changer la valeur de la focale rapidement voire run-time c'est que tu te rends bien compte de son rôle : plus la focale est grande, moins la perspective est forte et le point de fuite visible, à la limite f infinie tu retrouves une perspective isométrique/cavalière (tu obtiens (x,y) en faisant tendre f vers l'infini). A l'opposé plus la focale est faible et plus tout semble rapidement "aspiré" vers le point de fuite (tu obtiens (250,250) en faisant tendre f vers 0).

Tu peux même ensuite t'amuser à déplacer le point de fuite en prenant (x0,y0,-f) comme centre de la caméra (sans rien changer au reste).

Damien

Merci Damien,

Mon but (juste pour le fun) est de programmer la manipulation d'un objet 3D (un cube a la base), de pouvoir le faire tourner sur les trois plans (pour ca, j'ai deja la formule qui calcule l'angle entre deux points, il va juste falloir la travailler pour qu'elle calcule le point en fonction de l'angle)

Je posterai le projet si ca interesse quelqu'un

Mon plus gros soucis sur la perspective est que je voulais une approche qui respecte l'ordre de grandeur afin d'eviter toute deformation de l'objet dans la profondeur

Merci pour ton aide

par **Cliffe** » 28 Juil 2014, 21:54

C'est pour de la 3D ?
J'ai travailler une fois sur un pb où il fallait déplacer un objet sur un plan avec la souris :

[CENTER]

[/CENTER]

par **Carat** » 12 Aoû 2014, 10:22

Voila,
Je viens de terminer un petit prototype en C# - WPF: http://www.aliquid.be/3DStudio.rar

Le calcul de la perspective (basée sur l'approche de DamX) ne me satisfait pas... Si vous appliquez quelques rotations, puis que vous jouez avec la profondeur, vous remarquerez que l'objet à tendance à se deformer au fur et à mesure qu'il se rapproche du point de fuite...

Et lors d'un rapprochement, on a l'impression que le cube reste "plat"...

Si quelqu'un a une idée...

par **Cliffe** » 12 Aoû 2014, 17:24

Essaye avec ça : lien

par **Carat** » 13 Aoû 2014, 05:55

Cliffe a écrit:Essaye avec ça : lien

C'est exactement ça!!! La perspective est superbe dans ce binaire...
Pourrais-je te demander ton approche algo? ou la formule utilisée?

J'ai en attendant changé la formule de perspective qui me donne un bien meilleur résultat, mais encore avec quelques légères deformations:

new_point.X = this.m_vanishing_point.X - (this.m_vanishing_point.X - point.X) * Math.Pow(0.99925, point.Z);

new_point.Y = this.m_vanishing_point.Y - (this.m_vanishing_point.Y - point.Y) * Math.Pow(0.99925, point.Z);

par **fatal_error** » 13 Aoû 2014, 09:22

vous remarquerez que l'objet à tendance à se deformer au fur et à mesure qu'il se rapproche du point de fuite...

slt,

ca veut pas dire que c'est faux

le fait d'avoir un vecteur direction (dans laquelle l'oeil regarde), un plan de projection et des points dans l'espace ca reste quand même assez "naturel".
Pe t'es tu torché dans ton implémentation.

Comme tu veux juste faire tourner un cube, ca veut dire que ton plan de projection change pas.

L'approche algo est assez simple.
Soit un point O origine.
Soit le plan P de projection. Soit M un point qqconque de l'espace.
Tu veux prendre (OM), et projeter M sur P, idem trouver Mp appartient à (OM) et à P.
Comme tu veux pas déformer ta figure, tu prends O_p le point de P le plus proche de O.
Soit n = OO_p

soit (u_p,v_p) une base de P (vecteurs normés)

le plus simple c'est d'exprimer M' en fonction de u_p,v_p,O_p, puis considérer que ton canvas ben c'est le même plan que ton plan de projection. Donc de préférence u_p et v_p orthogonaux.., et n par définition.

OM = au+bv+cn
OM.u=au^2
d'ou tu récupères: OM=(OM.u, OM.v, OM.n/n.n), (produits scalaire), OM exprimé dans la base (O,u,v,n)
Tu déduis trivialement M', puisque M' appartient au plan P

Si OM.z <= 0: le point est derrière l'oeil, il faut faire un traitement particulier
Sinon
f=d(OO_p)
M' est tel que OM'.z = f
donc OM' = OM * f/OM.z

pour le cas ou OM.z<=0 c'est un peu plus délicat.
Ya un résultat qui dit que toute droite de l'espace est projeté en une droite projective (une droite dans le plan P). En particulier, pour une droite (AB) avec A devant l'oeil et B derrière l'oeil, tu projectes A sur P en A_p.

Tu prends l'intersection de B avec le plan parallèle à P passant par l'oeil. Soit B' ce point.
soit v=OB' la direction de la droite projective de (AB) (idem t'as la direction et tu multiplies par l'infini...ou un très grand nombre) et tu trouves B_p projection de B sur P par
A_pB_p= v
idem
B_p = v+A_p

et c'est tout!

par **Cliffe** » 14 Aoû 2014, 09:13

On utilise des matrices pour faire ce genre de manip ...

par **fatal_error** » 14 Aoû 2014, 18:11

Ah bon, même pour les vues à l'intérieur d'un volume?

Je suis curieux... :)

par **Cliffe** » 14 Aoû 2014, 18:36

fatal_error a écrit:Ah bon, même pour les vues à l'intérieur d'un volume?

Je suis curieux...

j'ai pas lu les msg. Mais il veux projeter un cube sur plan, donc matrice oui.

par **fatal_error** » 15 Aoû 2014, 08:33

j'ai pas lu les msg

oui ca je m'en doute

tout ce que j'ai fait peut se représenter par un calcul matriciel
projection dans la base (u,v,n), translation...

Mais il veux projeter un cube sur plan, donc matrice oui.

j'ai pas dit que c'était pas possible. En revanche, je m'interroge sur la possibilité du calcul matriciel pour la projection d'un cube sur un plan...quand on est à l'intérieur du dit cube.

par **Carat** » 17 Aoû 2014, 07:36

Merci à tous pour votre aide...

Va falloir avant toute chose que je me replonge dans les matrices... vu ça il y a plus de dix ans et plus jamais touché depuis... donc notions très très vagues...

par **fatal_error** » 17 Aoû 2014, 08:28

ben pour le coup, les matrices servent à rien de spécial...
si t'es capable de faire tes rotations de point, chose que tu as l'air d'avoir fait:
soit:
-(1) tu sais faire un produit matriciel
-(2) tu as fait tes rotations sans matrice

si (1) dans ce que là t'as rien de plus à apprendre
si (2) alors ya aucun sens à faire tes rotations à la main mais tes projections avec des matrices. et je suggèrerais de pas faire de calcul matriciel

Dans tous les cas une matrice de projection peut s'écrire
H, composée des vecteurs en colonne u,v,n
Soit M ton point dans R^3
HM donne ton point exprimé dans la base (u,v,n)
Tu peux vouloir faire une le produit d'une matrice (voir http://en.wikipedia.org/wiki/Transformation_matrix perspective projection),
ce qui donne la matrice de projection:

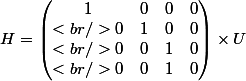
avec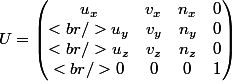

Soit M un point de l'espace

tu projettes :
M2=HM
et tu obtiens ton point dans le plan
avec M_p=M2*f/M2(4)

par **Cliffe** » 17 Aoû 2014, 11:14

ahah :ptdr:
Vous avez de drôle de façon de rechercher des info sur internet. Y'a des moteurs 3D qui existe déjà :id: (on est en 2014 les mecs).

Voilà : https://www.opengl.org/sdk/docs/man2/xhtml/gluPerspective.xml

Pourquoi vouloir refaire des choses qui ont déjà faites ?

par **Carat** » 17 Aoû 2014, 12:48

[quote="Carat"]...Mon but (juste pour le fun) est de programmer la manipulation d'un objet 3D (un cube a la base...[quote]

Je suis un fervent partisan du "avant d'utiliser un truc tout fait, cherches à le comprendre" :)
J'aime faire des petits prototypes, l'expérience m'a prouvé qu'ils finissaient toujours par être utile un jour ou l'autre... Et puis j'ai pas envie de mourir idiot, je suis un curieux de nature :)

par **fatal_error** » 17 Aoû 2014, 18:03

Je suis un fervent partisan du "avant d'utiliser un truc tout fait, cherches à le comprendre"

chercher à comprendre c'est un peu vague. Ca peut etre qu'est-ce que ca fait, comment c'est fait.
qu'est-ce que ca fait, vaut mieux savoir vu que si ca fait pas ce qu'on veut, ben ca sert à rien.
Mais surtout si ca fait plus que ce qu'on veut c'est ptet overkill

Mais de manière générale, je suis de plus en plus intéressé sur le comment c'est fait. Car j'en suis arrivé à la conclusion que si j'ai une idée de la chose, ca se comprend vite, et si je sais pas, alors c'est l'occasion d'apprendre!

bref:

Pourquoi vouloir refaire des choses qui ont déjà faites ?

- Déjà on fait pas la même chose, commence par lire la manière dont c'est fait en opengl.
- Ensuite, on fait un truc qui tient en une centaine de lignes (grossomodo), sans dépendances de librairies, sans dépendances de langage.
- On comprend ce qu'on fait.
- Et aussi, parce que c'est marrant de jouer avec l'infini. Et que c'est (pour moi) également marrant de jouer avec les lignes de fuites.

c'est certainement pas fait de la meilleure manière (mais il faut définir la meilleure manière) mais prétexter 2014 n'est certainement pas un argument valable... :hum:

Perspective conique en programmation

Perspective conique en programmation

Qui est en ligne