Bonjour Beagle, quel est l'interet de cette question qui te perturbe visiblement ?
Je ne suis pas GaBuZoMeu et cela ne m'empeche pas de comprendre qu'en appliquant 2 fois Thalès, le programme ne fonctionne pas.
Regardons ensemble d'où viennent les formules magiques du personnage imaginaire en appelant
)
Le code C++ (qui n'est pas sujet à interpretation, il ne s'est pas converti au dzlogisme pour lui fait plaisir) :
(x-x_v)}{y_v-y})
ce qui revient si
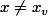
à
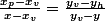
D'accord c'est Thales dans le triangle vert si on prolonge la verticale du point V en vert
(y-y_h)}{x_h-x})
ce qui revient si
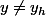
à

D'accord c'est Thales dans le triangle rouge si on prolonge l'horizontale du point H en rouge
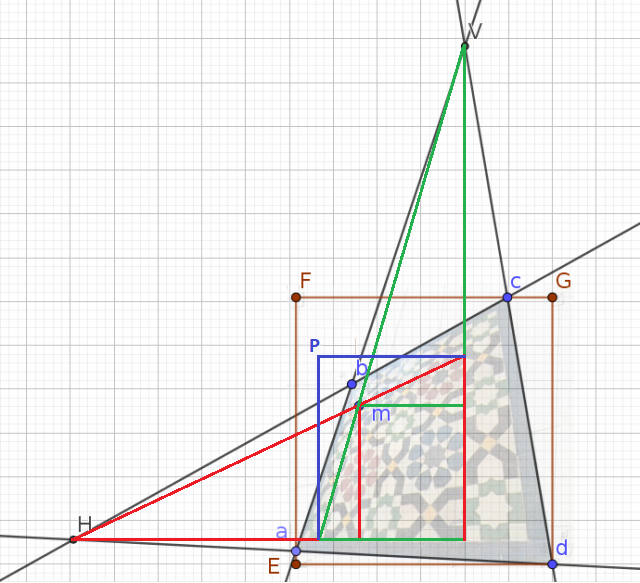
Sauf qu'il ne fait pas que cela, ensuite il corrige les cordonnées obtenues
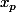
et
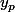
en calculant X et Y sans le dire à personne et sans comprendre pourquoi visiblement (mais s'il a une explication, qu'il la donne).
Je t'invite à relire le début de la discussion, la nécessité de préserver le birapport est quand même très bien expliquée même si dans la présentation initiale, le point d est laissé invariant contrairement à ce qui est fait dans le programme du personne imaginiaire. Même sans parler du niveau en maths des protagonistes :
D'un coté on a quelqu'un où il faut faire de la retroingénierie sur du code informatique pour donner un sens à ce qu'il raconte
De l'autre on a plusieurs personnes qui justifient parfaitement leurs formules et savent l'expliquer clairement.
Je te laisse toi et les lecteurs intéressés se faire leur propre opinion sur le fait que le premier se permet de critiquer avec véhémence la pédagogie des seconds et de s'offusquer quand on le corrige.
PS pour faire une analogie que tu connais : c'est exactement comme cette affreuse histoire de "loi uniforme qui aurait une répartition des écarts à la moyenne conforme à la loi normale", il manque quand même des mots dans la phrase pour que cela ait du sens du genre "fréquence" ou "nombre d’occurrence"... et c'est pas faute de lui avoir répété moi et d'autres des centaines de fois depuis le temps. OK pour faire l'effort de comprendre quelqu'un qui maitrise mal le vocabulaire spécifique aux maths encore faut-il que l'interlocuteur y mette de la bonne volonté et je suis d'accord avec la réponse de GaBuZoMeu sauf peut-être sur le mot "aimable" mais disons que c'était sans doute ironique

Modifié en dernier par Vassillia le 16 Fév 2021, 21:20, modifié 1 fois.

