Nombres de Catalan
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Science
- Membre Relatif
- Messages: 228
- Enregistré le: 04 Fév 2008, 18:50
-
 par Science » 19 Mai 2010, 15:58
par Science » 19 Mai 2010, 15:58
Bonjour : une des applications des nombres de catalan est le nombre de possibilités de découpage d'un polygone convexe à n diagonales (c'est à dire n+2 côtés) en triangle : ce nombre est

. Voilà ma question : en cours le prof nous a dit que

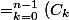(C_(n-k-1)))
mais ce que je ne comprends pas c'est pourquoi? Je suis dessus depuis plusieurs jours et je ne trouve pas la réponse.
Merci de votre aide
Cordialement
Science
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Mai 2010, 16:15
par Nightmare » 19 Mai 2010, 16:15
Salut,
lorsque je fais mon découpage, j'obtiens forcément un triangle de sommets les deux derniers du polygone et un 3ème. Si on retire ce triangle, il ne reste qu'à découper deux sous-polygone : L'un qui a k sommets (où k est le numéro du sommet considéré dans le triangle qu'on a retiré) et l'autre qui en a n-k-1
:happy3:
-
Science
- Membre Relatif
- Messages: 228
- Enregistré le: 04 Fév 2008, 18:50
-
 par Science » 19 Mai 2010, 16:19
par Science » 19 Mai 2010, 16:19
Nightmare a écrit:Salut,
lorsque je fais mon découpage, j'obtiens forcément un triangle de sommets les deux derniers du polygone et un 3ème. Si on retire ce triangle, il ne reste qu'à découper deux sous-polygone : L'un qui a k sommets (où k est le numéro du sommet considéré dans le triangle qu'on a retiré) et l'autre qui en a n-k-1
:happy3:
Mais à ce moment là ca devrait être plutôt
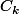
+
+1)
non ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 19 Mai 2010, 16:43
par Doraki » 19 Mai 2010, 16:43
non, il faut compter le nombre de manières de séparer le polygone en triangles,
alors que là dans ta formule j'ai l'impression que tu comptes le nombre de triangles dans la décomposition.
Pourquoi tu additionnes, et surtout, pourquoi y'aurait un +1 ?
-
Science
- Membre Relatif
- Messages: 228
- Enregistré le: 04 Fév 2008, 18:50
-
 par Science » 19 Mai 2010, 17:06
par Science » 19 Mai 2010, 17:06
Doraki a écrit:non, il faut compter le nombre de manières de séparer le polygone en triangles,
alors que là dans ta formule j'ai l'impression que tu comptes le nombre de triangles dans la décomposition.
Pourquoi tu additionnes, et surtout, pourquoi y'aurait un +1 ?
La réponse est dans la question : effectivement j'ai fais l'erreur de compter le nombre de triangles dans la décomposition :ptdr:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités