Les plus jolies démonstrations selon vous? D'ail

[Bastien L.]

Bonjour à tous!


Je réalise en ce moment une sorte de sondage, à savoir, je me demande quelles sont selon les matheux (qu'ils soient experts ou simples amateurs) les plus jolies démonstrations dans cette matière. Qu'est-ce qu'une jolie démonstration? J'ai ma petite idée là-dessus, mais c'est à chacun de voir… D'ailleurs, si certains veulent tenter d'exprimer ce que c'est pour eux qu'une jolie démonstration, ce sera encore mieux… ^^

Une dernière chose, originellement, je posais la question à des copains de terminale, donc, si vous citez celle du grand théorème de Fermat (par exemple), voudriez-vous bien citer aussi une démonstration accessible pour un (bon) lycéen? Pas forcément au programme, mais accessible… ^^ Merci… :-)

Pour info, jusqu'à présent, j'ai obtenu la démonstration par récurrence de la "formule" qui donne la somme des entiers naturels jusqu'à n, la démonstration "sans monstration" par disjonction des cas que a^b peut être rationnel sans que ni a ni b ne le soient (celle qui utilise racine de 2 exposant racine de 2), la démonstration par l'absurde de l'irrationnalité de la racine carrée de 2, la démonstration par l'absurde de l'existance d'une infinité de nombres premiers. Voilà! À vous! :-)

[JonathanMath9]

Salut. pour moi, une bonne demonstration, c'est quand tout le cheminement se fait a partir de pas grand chose, et au final, on arrive a une reponse complete.

Des demo aui me plaisent specialement, c les demo des theoreme de geometrie, et celles de trigono (formules additions, duplication, simpsons, etc)

[Bastien L.]

Merci… :-) Je pense en effet qu'on est toujours émerveillé de voir tout ce que la pensée peut construire avec pas grand-chose à sa disposition…
Pourrais-tu, s'il-te-plaît, dégager un exemple précis, le plus représentatif pour toi? Merci… :-)

[JPzarb]

Bonjour,
Pour ma part, je ne suis pas mathématicien mais physicien. Cependant, je me suis fait un idée (qui m'est propre) de l'esthétisme mathématique. Donc de mon point de vue, une jolie démonstration est une démonstration qui ne s'enorgueillit pas d'un formalisme trop complexe. Un mathématicien est un partisan du moindre effort, dans le sens où, s'il existe plusieurs cheminement pour arrivé à une solution, le matheux cherchera le plus simple (même s'il n'est pas le plus évident).

Donc outre les démonstrations que tu as déjà citées, il y en a une assez joli, qui est la résolution d'un des plus anciens problème de géométrie (si ce n'est LE plus ancien)... Tu vois de quoi je parle ? ... Eh oui, la quadrature du cercle !
Une démonstration qui se fait à travers plusieurs autres démonstration (démonstration de l'éxistence des nombre transcendant, de la transcendence de pi ...)

Si tu admet dans un premier temps certains théorèmes, le démonstration de l'impossibilité de la quadrature du cercle est très accessible.

En second lieu, plus en rapport avec le programme, je citerais aussi la démonstration (par récurence) du binome de Newton.

Voila ^^

A bientot

ps : Problème de la quadrature du cercle : Construre un carré de même aire qu'un cercle donné... UNIQUEMENT avec une règle et un compas.
Notions (théorèmes) nécessaires : Constructibilité des nombre, existence des nombres transcendants (nombre qui ne sont racine d'aucun polynomes), et transcendence de pi. (je crois que c'est tout... Mais à vérifier).

[SimonB]

Notions (théorèmes) nécessaires : Constructibilité des nombre, existence des nombres transcendants (nombre qui ne sont racine d'aucun polynomes), et transcendence de pi. (je crois que c'est tout... Mais à vérifier).

Euh, juste la transcendance de (l'existence des nombres transcendants en découle mais ça n'est pas utile en soi !). Et le théorème de Wantzel sur la constructibilité. C'est un très joli théorème, l'impossibilité de la quadrature du cercle, mais plus, à mon sens, en tant que résultat plutôt qu'en tant que preuve. Les preuves font intervenir des notions d'analyse (pour la transcendance) et d'algèbre (pour Wantzel) assez poussées, et je ne pense pas qu'en terminale ça présente un intérêt quelconque.

Dans les belles démonstrations, je classerais plutôt celles qui ne font appel qu'à très peu de concepts, comme celles qui utilisent le principe des tiroirs (si n chaussettes sont placées dans r tiroirs et n>r, alors il existe un tiroir qui contient au moins deux chaussettes). Ce principe permet de prouver :
-que si l'on choisit (n+1) entiers entre 1 et 2n, il y en a 2 qui sont premiers entre eux
-qu'il y en a aussi deux tels que l'un est multiple de l'autre
et bien d'autres choses a priori pas si triviales...

[Bastien L.]

Tiens! Marrant, le principe des tirroirs… :-) En revanche, je ne vois pas comment il permet de démontrer les deux propositions que tu as écrites… :hein:

[Imod]

Pour moi , le top du top ce sont les démonstrations de Cantor qui tiennent souvent en deux lignes , exemples :
1°) Il n'existe pas d'ensemble contenant tous les ensembles .
2°) Aucun ensemble n'est en bijection avec l'ensemble de ses parties .

Imod

[Bastien L.]

Où peut-on les trouver?

[uztop]

Salut,

il y a un resultat bien connu et que j'aime bien dont la demo est accessible en terminale: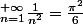
La demo accessible au lycee passe par les integrales de Wallis; ce n'est pas tellement la demo qui est belle en soi, mais le resultat. Moi, ca m'avait fascine de voir apparaitre des comme limite de cette somme, je ne m'y attendais pas du tout

[Bastien L.]

Je partage ton étonnement…*^^

[JPzarb]

Re bonjour,

Un truc marrant aussi et assez accessible (je ne sais pas si quelqu'un en a deja parlé) :

http://fr.wikipedia.org/wiki/Racine_carr%C3%A9e#Curiosit.C3.A9s

CHAPITRE : "CURIOSITE"

A voir

A bientot

[Bastien L.]

:marteau: Tu veux nous tuer? lol Pour ma part, je décroche dès le "Pour des raisons analogues, on obtient" de la troisième ligne, car si 2 est égal à la racine de (2+2), 3 n'est pas égal à la racine de (3+3), donc je ne vois pas ce qu'il y a d'analogue… Enfin, ça me fait peur, tout ça…*^^

[Euler911]

hum...
3=V(6+3)...!!!

[Zweig]

Salut,

Tiens! Marrant, le principe des tirroirs… En revanche, je ne vois pas comment il permet de démontrer les deux propositions que tu as écrites… :hein:

-que si l'on choisit (n+1) entiers entre 1 et 2n, il y en a 2 qui sont premiers entre eux
-qu'il y en a aussi deux tels que l'un est multiple de l'autre

- Soit l'ensemble des entiers de à . On partitionne cet ensemble en sous-ensembles disjoints constitués de deux entiers consécutifs : 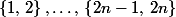. Clairement, on dispose de sous-ensembles ("tiroirs") et de 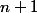nombres choisis ("objets"). Donc d'après le principe de Dirichlet, deux de ces nombres sont dans le même sous-ensemble, et comme deux entiers consécutifs sont premiers entre eux, la conclusion s'ensuit.

- Tout nombre entier naturel s'écrit sous la forme n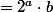 (conséquence directe de la décomposition en produit de facteurs premiers) avec un entier naturel impair. On partitionne en sous-ensembles disjoints :






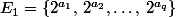
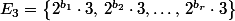
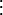
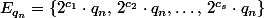
avec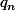 le plus grand entier impair inférieur à .

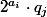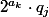Comme il y a entiers impairs dans , nous disposons donc de "tiroirs" (ces sous-ensembles) et de "objets". Ainsi d'après le principe de Dirichlet, deux des nombres choisis sont dans le même sous-ensemble, c'est-à-dire, il en existe forcément deux de la forme et avec 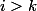. Clairement donc, l'un est multiple de l'autre.

[Bastien L.]

Joli, très joli… :-)

P.-S.: Pour Euler911: je reconnais: :stupid_in

[JonathanMath9]

Merci… Je pense en effet qu'on est toujours émerveillé de voir tout ce que la pensée peut construire avec pas grand-chose à sa disposition…
Pourrais-tu, s'il-te-plaît, dégager un exemple précis, le plus représentatif pour toi? Merci…

La demonstration qui m a plu particulierement, c la demo de : lim quand x tend vers 0 de sinx sur x. cette demo m a remontre tout le savoir faire des mathematiques.

et toi, celle qui ta le plus plu, c laquelle?

[Bastien L.]

Bonsoir JonathanMath9!


Il existe plusieurs manières, plus ou moins longues, de prouver ce que tu dis, alors, à laquelle penses-tu, s'il-te-plaît? :-)

Moi, je pense spontanément à des démonstrations qui disent beaucoup, voire énormément, en peu de mots. Des démonstrations qui montrent à quel point par les mathématiques nous sommes capables de dépasser la finitude et la discretion de notre propre pensée. Voilà pourquoi j'ai cité la démonstration par récurrence de la "formule" de la somme des entiers de 1 à n, la magnifique démonstration du fait que a^b peut être rationnel sans que ni a ni b ne le soit, faisant intervenir racine de 2 avec une disjonction des cas, et, pour finir, la démonstration par l'absurde de l'existance d'une infinité de nombres premiers. Voilà! Selon ce que j'ai écrit, il n'est pas étonnant de trouver de la récurrence et de l'absurde… ^^ J'aime aussi beaucoup la démonstration par l'absurde de l'irrationnalité de racine de 2 et celle de l'inégalité triangulaire avec l'intégrale. :-)

[Joker62]

Niveau irrationnalité de racine(2), Léon a ouvert un post vraiment intéressant qui réunit pas mal de preuve :)

[Bastien L.]

Oui, elle est très intéressante, cette discussion, même si certaines choses me sont hors de portée… :-) C'est toujours sympa, comme travail…

[Joker62]

Bon sinon pour ma part, j'aime les démonstrations qui se servent d'autre branche des mathématiques :)
Comme par exemple cité plus haut, la transcendance de pi qui est un résultat algébrique et qui se fait avec les outils analytiques.