Salut,
Je comprend absolument pas ce que ça peut vouloir dire ça :
FLBP a écrit: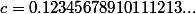
Qui réunit les nombres naturels jusqu'à

(tendant vers l'infini) à la suites. Les nombres univers sont donc des permutations de ces

nombres.
- Déjà, dans la constante en question, ben y'a rien qui se nomme "n", vu qu'on prend TOUT les entiers naturels donc une "permutation de ces n nombres", ça veut rien dire.
- Ensuite, un "nombre univers", on doit trouver n'importe quelle suite de chiffres à un endroit ou un autre de ces décimales, mais bien évidement, rien ne te dit que cet endroit est unique, bien au contraire (la même suite de décimale est forcée d'apparaitre une infinité de fois dans les décimales d'un nombre univers). Donc les nombres univers ne s'obtiennent absolument pas tous en écrivant "dans un ordre quelconque" la liste des nombres entiers (i.e. en "permutant" ces "n" nombres).
- Sans parler du fait que, bien évidement, face à un réel donné écrit sous forme décimale (infinie), tu a des tonnes et des tonnes de façon de découper les décimales pour en faire une liste de nombre entiers donc l'opération qui consiste, partant d'une suite (infinie) de nombres entiers à les mettre "bout à bout" pour faire les décimales d'un réel, c'est absolument pas du tout bijectif.
FLBP a écrit:Imaginons le plus simple ensemble des permutations de la constante de Champernowne, l'ensemble

, 0 y compris :
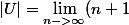!)
Et ça, c'est "encore plus" du grand n'importe quoi :
- La suite (n+1)!, elle est divergente et lorsque l'on écrit qu'elle "tend vers +oo", ça veut dire un truc bien précis (c.f. la définition d'une suite qui tend vers +oo) et ça ne fabrique absolument pas un "nouvel objet" qui s'appellerait "+oo". Bref, le symbole +oo utilisé dans le contexte des limites, c'est pas un réel, et c'est pas un cardinal non plus (au sens de la théorie des cardinaux). Donc le cardinal de U, ça a aucune chance d'être égal à ça.
- De plus, si on tente d'interpréter ton truc de façon à lui donner du sens, c'est à dire en regardant les (n+1)! comme des cardinaux et la limite comme étant le cardinal de la réunion d'enssembles de cardinal (n+1)! alors le résultat est complètement faux : le cardinal d'une réunion dénombrable d'ensemble fini, c'est le dénombrable alors que le cardinal des bijections de N dans N (ton U), il a la puissance du continu.
Et cette (énorme) différence provient du fait qu'une bijection quelconque de N->N, il est bien clair que c'est pas forcément une bijection de {0..n} dans {0..n} qu'on a complété avec l'identité les i>n.
Bref, l'ensemble des bijections de N->N, c'est beaucoup beaucoup plus gros que la réunion des ensemble de bijections de {0..n} dans {0..n}.
Et évidement, toute la suite axée sur ce type de raisonnement mélangeant alègrement et sans le moindre discernement les notions de limites (de suites divergentes) et celles de cardinal (infini) n'a pas le moindre sens mathématique.
