Les 4444

[morpho]

On dispose quatre 4 et 7 oppérations { +, -, x, /, , , !=factoriel }, exprimer 39 en fonction des 4444 et avec uniquement ces 7 opérations.

Exemple:
0 = 4 - 4 + 4 - 4
1 = 4/4 + 4 - 4
2 = 4/4 + 4/4
10 = (44 -4)/4











i relié avec les 4444




etc...

Question: 39 = ????

[chan79]

salut

[chan79]

On dispose quatre 4 et 7 oppérations { +, -, x, /, , , !=factoriel }, exprimer 39 en fonction des 4444 et avec uniquement ces 7 opérations.

Exemple:
0 = 4 - 4 + 4 - 4
1 = 4/4 + 4 - 4
2 = 4/4 + 4/4
10 = (44 -4)/4











i relié avec les 4444




etc...

Question: 39 = ????

Solution de Gérard Villemin sur son site
4! + (4!/(.4*4)) si on accepte l'omission du 0

[morpho]

Solution de Gérard Villemin sur son site
4! + (4!/(.4*4)) si on accepte l'omission du 0

Oppération .4 non autorisée (sinon c'est trop facile!)
On utilise uniquement ces 7 opérations (pas 8 opérations)

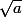
REMARQUE IMPORTANTE: C'est comme pour les nombres constructibles, on part de Q et avec les operations { +,-,x,/ , } , quels sont des nombres qu'on peut atteindre ?
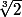
est il constructible ? s il n'est pas constructible alors il faut le démontrer, on n'ajoute pas une 6eme opération pour qu'il le soit !!!!

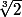
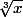
Attention dire que est non constuctible sous prétexte qu'il porte le symbole c'est faux car est bien un nombre constructible

Pour les quatre 4, les gens ajoutent souvent une 8eme opération du genre: [x], i², 4°, .4=4/10, gamma(4), ... pour pouvoir exprimer les nombres qui semblent difficiles à exprimer avec les 7 opérations ci-dessus. Mais ce n'est pas vraiment une bonne stratégie de recherche.

=============
Bref, les entiers entre 0 et 50 sont tous quatrix (exprimable en 4444) sauf le 39, il est vraiment étonnant que le 39 résiste .... si on prend les entiers entre 0 et 100 il y a 18 nombres non-quatrix
39, 53, 55, 57, 59, 61, 67, 69, 71, 73, 75, 77, 79, 83, 85, 87, 89, 91
On pourrait donc emettre la conjecture suivante:
les nombres suivants ne sont pas quatrix:
39, 53, 55, 57, 59, 61, 67, 69, 71, 73, 75, 77, 79, 83, 85, 87, 89, 91