Bonjour à tous, j'aimerais démontrer une proposition mais je n'ai pas trop de pistes... auriez vous des idées ?
La proposition est la suivante:
A et B sont deux matrices carrées de même dimension inversibles dont la somme est inversible;
alors la somme de leurs inverses est également inversible.
Voilà, c'est tout, merci d'avance pour vos réponses !
Inversion de somme de matrices inversibles
4 messages
- Page 1 sur 1
Re: Inversion de somme de matrices inversibles
Hello,
M est inversible équivaut à det(M) non nul.
Puisque A et B sont inversibles, on a:
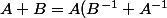B)
Par multiplicativité du déterminant, on a le det de la somme des inverses qui vaut:
Det(A+B)/det(A)det(B) qui est non nul
M est inversible équivaut à det(M) non nul.
Puisque A et B sont inversibles, on a:
Par multiplicativité du déterminant, on a le det de la somme des inverses qui vaut:
Det(A+B)/det(A)det(B) qui est non nul
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Inversion de somme de matrices inversibles
Salut,
Et on peut tout à fait se passer de la notion de déterminant (ce qui en particulier montre que le résultat est valable sur n'importe quel anneau) :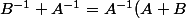B^{-1}) est le produit de 3 éléments inversible donc il est inversible (et son inverse est
est le produit de 3 éléments inversible donc il est inversible (et son inverse est ^{-1}A) )
)
Et on peut tout à fait se passer de la notion de déterminant (ce qui en particulier montre que le résultat est valable sur n'importe quel anneau) :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
