Bonjour à tous,
je me pose quelques questions auxquelles je ne trouve pas de réponse
en vrac, les voici:
e^1 = 2.718 environ, comment ce nombre a-t-il été choisi ? comment l'as-t-on découvert ?
à quoi est égale la fonction ln(x) ? quelle opération fait la calculatrice pour calculer ln(4) par exemple ? = comment calculer moi-même ln(4) ?
et quelle est la différence entre ln(x) et la fonction log ?
Merci beaucoup d'avance !
Interrogations générales sur logarithmes et fonctions e^x
4 messages
- Page 1 sur 1
Re: Interrogations générales sur logarithmes et fonctions e^
Salut,
Le logarithme néperien, l'une des façon de le définir, c'est de dire que c'est l'unique primitive s'annulant en t=1 de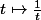 .
.
Si tu n'as pas vu ce qu'est une primitive, ça signifie que, si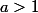 ,
, ) c'est la surface comprise entre les droites d'équation
c'est la surface comprise entre les droites d'équation  et
et  , au dessus de l'axe des
, au dessus de l'axe des  , en dessous de la courbe de
, en dessous de la courbe de 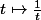 (fait un dessin, j'ai la flemme...)
(fait un dessin, j'ai la flemme...)
Et le réel (*) c'est la valeur qu'il faut prendre pour que
(*) c'est la valeur qu'il faut prendre pour que =1) , c'est à dire la valeur qu'il faut prendre pour
, c'est à dire la valeur qu'il faut prendre pour  dans la définition ci-dessus pour que la surface fasse précisément
dans la définition ci-dessus pour que la surface fasse précisément  . Ca permet déjà de voir le réel
. Ca permet déjà de voir le réel  comme ayant une propriété "remarquable" (surface sous la courbe =1).
comme ayant une propriété "remarquable" (surface sous la courbe =1).
Un autre point de vue (qui en fait est le même mais il faut un petit calcul pour s'en apercevoir), c'est que, pour tout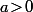 et tout
et tout  réel on arrive à définir la quantité
réel on arrive à définir la quantité 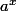 (sans utiliser ni log ni exponentielle : c'est un peu chiant, mais faisable...) et on peut montrer que la dérivée de la fonction
(sans utiliser ni log ni exponentielle : c'est un peu chiant, mais faisable...) et on peut montrer que la dérivée de la fonction 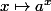 est une fonction de la forme
est une fonction de la forme 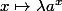 où
où  est une constante qui dépend de
est une constante qui dépend de  . Évidement, on se dit que ça serait pas con de prendre
. Évidement, on se dit que ça serait pas con de prendre  de façon à ce que la constante
de façon à ce que la constante  soit la plus simple possible et, en fait, si on veut que
soit la plus simple possible et, en fait, si on veut que 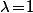 , ben il faut prendre
, ben il faut prendre  ce qui le rend de nouveau "remarquable".
ce qui le rend de nouveau "remarquable".
Dixit Wiki, "Ce nombre est défini à la fin du XVIIe siècle, dans une correspondance entre Leibniz et Christian Huygens comme étant la base du logarithme naturel."
Concernant "à quoi est égale la fonction ln(x)", tu as une des réponse possible ci dessus (i.e. surface sous la courbe de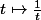 ) et il y en aurai de nombreuses autres.
) et il y en aurai de nombreuses autres.
Je ne sais pas précisément comment fait la calculette pour calculer ln(x) vu qu'il y a beaucoup de méthodes possible plus ou moins compliquées à mettre en œuvre. J'opterais bien pour le fait qu'elle connait "par cœur" quelques valeurs (une dizaine ? plus ?) et qu'elle a un algorithme pour en déduire les valeurs de toute les autres à partir de celles là.
A la main, c'est pareil, il y a des tas de méthodes plus ou moins compliquées (et en conséquence plus ou moins rapides...) Une qui n'est pas compliquées du tout (et pas rapide du tout...), c'est d'estimer la surface sous la courbe en la découpant approximativement en un certain nombre de rectangles.
Enfin, pour comprendre la différence entre le logarithme népérien) et le logarithme décimal
et le logarithme décimal ) , le plus simple, c'est de faire le lien entre les deux premiers paragraphes ci dessus : lorsque tu te donne un
, le plus simple, c'est de faire le lien entre les deux premiers paragraphes ci dessus : lorsque tu te donne un 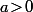 , la fonction
, la fonction 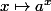 est appelée exponentielle de base a et sa bijection réciproque
est appelée exponentielle de base a et sa bijection réciproque ) est appelé logarithme de base a (donc, par définition,
est appelé logarithme de base a (donc, par définition, 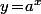 si et seulement si
si et seulement si 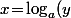) ).
).
Le log népérien correspond à et le log décimal correspond à
et le log décimal correspond à 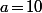 .
.
Mais on peut aussi utiliser des log en d'autre base. Par exemple, très naturellement, en informatique, on utilise le logarithme de base 2.
(*) Parfois appelé "constante de Néper" ou bien "nombre d'Euler", mais ce dernier nom est un peu pourri vu qu'il y a d'autres trucs qui s'appellent les "nombres d'Euler" et même une "constante d'Euler" qui n'ont que peu de rapport avec .
.
Le logarithme néperien, l'une des façon de le définir, c'est de dire que c'est l'unique primitive s'annulant en t=1 de
Si tu n'as pas vu ce qu'est une primitive, ça signifie que, si
Et le réel
Un autre point de vue (qui en fait est le même mais il faut un petit calcul pour s'en apercevoir), c'est que, pour tout
Dixit Wiki, "Ce nombre est défini à la fin du XVIIe siècle, dans une correspondance entre Leibniz et Christian Huygens comme étant la base du logarithme naturel."
Concernant "à quoi est égale la fonction ln(x)", tu as une des réponse possible ci dessus (i.e. surface sous la courbe de
Je ne sais pas précisément comment fait la calculette pour calculer ln(x) vu qu'il y a beaucoup de méthodes possible plus ou moins compliquées à mettre en œuvre. J'opterais bien pour le fait qu'elle connait "par cœur" quelques valeurs (une dizaine ? plus ?) et qu'elle a un algorithme pour en déduire les valeurs de toute les autres à partir de celles là.
A la main, c'est pareil, il y a des tas de méthodes plus ou moins compliquées (et en conséquence plus ou moins rapides...) Une qui n'est pas compliquées du tout (et pas rapide du tout...), c'est d'estimer la surface sous la courbe en la découpant approximativement en un certain nombre de rectangles.
Enfin, pour comprendre la différence entre le logarithme népérien
Le log népérien correspond à
Mais on peut aussi utiliser des log en d'autre base. Par exemple, très naturellement, en informatique, on utilise le logarithme de base 2.
(*) Parfois appelé "constante de Néper" ou bien "nombre d'Euler", mais ce dernier nom est un peu pourri vu qu'il y a d'autres trucs qui s'appellent les "nombres d'Euler" et même une "constante d'Euler" qui n'ont que peu de rapport avec
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Interrogations générales sur logarithmes et fonctions e^
Pour compléter la belle réponse apportée par Ben,
on peut montrer que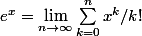 et donc
et donc
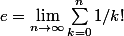 .
.
On peut aussi le faire apparaître avec des histoires de taux d'intérêt et de durée d'investissment mais j'ai un peu la flemme de l'écrire...
Bon sinon le fait que l'exponentielle soit égale à sa dérivée fait qu'on la voit apparaître dans énormément de modélisation de la réalité (problème de mécanique, d'électronique, d'équilibre chimique, d'évolution de population...).
on peut montrer que
On peut aussi le faire apparaître avec des histoires de taux d'intérêt et de durée d'investissment mais j'ai un peu la flemme de l'écrire...
Bon sinon le fait que l'exponentielle soit égale à sa dérivée fait qu'on la voit apparaître dans énormément de modélisation de la réalité (problème de mécanique, d'électronique, d'équilibre chimique, d'évolution de population...).
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Interrogations générales sur logarithmes et fonctions e^
Bonjour,
tu peux aussi aller voir :
https://fr.wikipedia.org/wiki/Logarithme_naturel
et http://www.maths-et-tiques.fr/index.php/histoire-des-maths/nombres/le-nombre-e
Pour le calcul, dans le premier lien que j'ai donnée ils donnent deux formules :
-La série de Mercator (mais ça vitesse de convergence est très très lente )
)
-ou alors la formule suivante := \sum_{k=0}^{+\infty}{2\over{2k+1}}\left({y-1}\over{y+1}\right)^{2k+1})
Donc par exemple pour ln(4), en calculant la somme des deux premier termes on obtient :
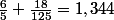
et tu as déjà le "1,3" de juste. Plus tu iras loin dans le calcul de la somme, plus le résultat sera précis.
tu peux aussi aller voir :
https://fr.wikipedia.org/wiki/Logarithme_naturel
et http://www.maths-et-tiques.fr/index.php/histoire-des-maths/nombres/le-nombre-e
Pour le calcul, dans le premier lien que j'ai donnée ils donnent deux formules :
-La série de Mercator (mais ça vitesse de convergence est très très lente
 )
)-ou alors la formule suivante :
Donc par exemple pour ln(4), en calculant la somme des deux premier termes on obtient :
et tu as déjà le "1,3" de juste. Plus tu iras loin dans le calcul de la somme, plus le résultat sera précis.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
