Bonjour
Je suis complètement paumé là car en faisant du dessin je me suis rendu compte de quelque chose d'étrange cette nuit
Je ne sais pas si c'est exact et si c'est exact je n'ai aucune idée de comment démontrer cela
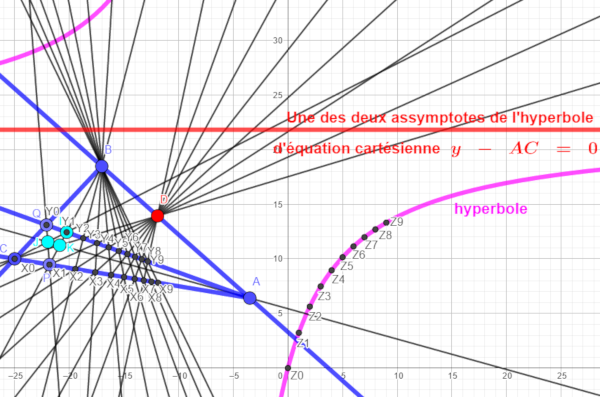
Voilà l'énoncé et la figure et j'ai beau bouger les points

les points

sont toujours sur une hyperbole dont une des deux assymptotes est d'équation
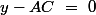
Je m'explique bien que l'hyperbole passe par le point (0,0)
et je m'explique bien l'équation de l'une de ces deux assymptotes mais je ne m'explique pas pourquoi les points

sont tous sur une même hyperbole
----------------------
Énoncé
On se place dans le plan affine euclidien
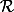
est un repère cartésien orthonormé et

est un triangle non plat
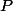
est un point de la demi-droite notée

d'origine

passant par

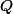
est un point de la demi-droite notée

d'origine

passant par

Les points

sont distincts deux à deux
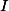
est l'intersection de la droite
\)
et de la demi-droite notée

d'origine

passant par

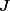
est l'intersection des deux droites
\)
et
\)
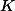
est l'intersection des deux droites
\)
et
\)
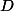
est l'intersection des deux droites
\)
et
\)
_{i\in \mathbb {N}}\)
une famille dénombrable de points de la droite

On pose
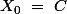
et

_{i\in \mathbb {N}}\)
une famille dénombrable de points de la droite

On pose
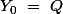
et
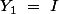
Les autres points de ces deux familles sont définis par
\ \cap \ \Delta \ ,\ X_i\ =\ \left(BY_i\right)\ \cap \ \Delta _A)
Enfin
_{i\in \mathbb {N}}\)
une famille dénombrable de points dont les coordonnées cartésiennes par rapport au repère
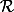
sont définies par
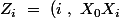\)
Alors (conjecture pour l'instant)
Les points

appartiennent à la même hyperbole dont l'une des deux assymptotes est la droite d'équation cartésienne
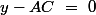
Figure