Est-ce logique ??

[nada-top]

salut,

je suis pas sure si on peut raisonner ainsi :
on a une proposition dont on veut démontrer la véracité .

• supposer que 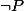est vraie .
  
• trouver un contre exemple .
  
• en déduire la fausseté de 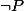i.e la véracité de .
  

est-ce logique ?

[nuage]

Salut,
c'est logique : principe du tiers exclu.
Si la négation d'une proposition est fausse alors la proposition est vraie.
En pratique (mathématique) il faut faire attention au moment de la négation.
A+

[nada-top]

c'est logique : principe du tiers exclu.
Si la négation d'une proposition est fausse alors la proposition est vraie.

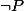
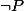
oui c'est évident mais dont je suis pas sure c'est la manière de prouver la fausseté de : supposer que est vraie puis trouver un contre exemple !

est-ce toujours logique .?

[nuage]

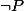
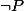
oui c'est évident mais dont je suis pas sure c'est la manière de prouver la fausseté de : supposer que est vraie puis trouver un contre exemple !

est-ce toujours logique .?

Oui, mais je me répéte, fais attention à la négation !
En général, si il y a des erreurs, c'est là qu'elles se produisent.

A+

[nada-top]

merci nuage

mais tu peux me donner un exemple simple ou on applique ce raisonnemet ? ça me parait un peu illogique car sera trés facile de trouver un contre exemple à une proposition qu'on est sûr de sa fausseté .

[nuage]

Salut,
un exemple :
Soit P la proposition :
"il y a un nombre infini de nombres premiers"
Sa négation est :
"il existe N tel que tous les nombres premiers soient inférieurs à N"
Il est facile de voir que N!+1 a un diviseur premier supérieur à N.
La négation de P est fausse donc P est vraie : il y a une infinité de nombres premier.

[nada-top]

Ah oui je vois tout ce qui compte c'est la négation .

merci nuage pour ces précisions :happy3: