Des suites et séries de fonctions
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Elerinna
- Membre Rationnel
- Messages: 559
- Enregistré le: 27 Fév 2012, 18:59
-
 par Elerinna » 07 Mar 2012, 16:57
par Elerinna » 07 Mar 2012, 16:57
Soit :
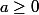
, et
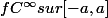
On suppose que :
 \geq 0)
.
Montrer que f est développable en série entière sur
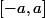
.

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 08 Mar 2012, 01:13
par nuage » 08 Mar 2012, 01:13
Elerinna a écrit:Soit :
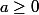
, et
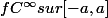
On suppose que :
 \geq 0)
.
Montrer que f est développable en série entière sur
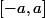
.
par exemple
=\text{e}^{-\frac1{x^2} }\text{ si } x\neq 0 \text{ et } f(0)=0)
-
Elerinna
- Membre Rationnel
- Messages: 559
- Enregistré le: 27 Fév 2012, 18:59
-
 par Elerinna » 08 Mar 2012, 10:09
par Elerinna » 08 Mar 2012, 10:09
La démonstration est validée par la généralisation de la preuve et démontée par le contre-exemple. :dodo:
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 08 Mar 2012, 12:47
par Judoboy » 08 Mar 2012, 12:47
Elerinna a écrit:La démonstration est validée par la généralisation de la preuve et démontée par le contre-exemple. :dodo:
Nan mais je crois que là il vient de donner un contre-exemple en fait.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 08 Mar 2012, 15:41
par Doraki » 08 Mar 2012, 15:41
Judoboy a écrit:Nan mais je crois que là il vient de donner un contre-exemple en fait.
ce n'est pas un contre-exemple vu qu'il ne vérifie pas les hypothèses de l'énoncé (sauf si a=0, et alors l'énoncé ne veut plus dire grand chose et on a quand même f = 0 sur [0;0])
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 08 Mar 2012, 17:26
par Judoboy » 08 Mar 2012, 17:26
Ca remonte à longtemps mais de mémoire en maths spé c'était l'exemple typique de la fonction Cinfini non développable en série entière. Et j'ai bien l'impression que toutes les dérivées paires sont positives.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 08 Mar 2012, 18:09
par Doraki » 08 Mar 2012, 18:09
ben si je ne m'abuse, sa dérivée seconde est du signe de (4-6x²), qui n'est pas tout le temps positif, loin de là.
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 08 Mar 2012, 18:26
par Judoboy » 08 Mar 2012, 18:26
Doraki a écrit:ben si je ne m'abuse, sa dérivée seconde est du signe de (4-6x²), qui n'est pas tout le temps positif, loin de là.
Au temps pour moi, mais du coup je comprends pas le message de nuage...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 08 Mar 2012, 18:43
par Nightmare » 08 Mar 2012, 18:43
A mon avis, nuage a pris le 2n comme un exposant et non comme une dérivée 2n-ème.
-
Elerinna
- Membre Rationnel
- Messages: 559
- Enregistré le: 27 Fév 2012, 18:59
-
 par Elerinna » 09 Mar 2012, 10:56
par Elerinna » 09 Mar 2012, 10:56
L'exercice généralise l'étude des fonctions complètement
convexes, i.e.
} \geq 0)
. Faire
un DL de f.
-
SimonB
 par SimonB » 09 Mar 2012, 18:09
par SimonB » 09 Mar 2012, 18:09
Pour les curieux, il s'agit d'un théorème dit "de Bernstein" (et c'est un développement classique pour un agrégatif).
Un exemple d'une telle fonction (parce que ça n'est pas vraiment évident à trouver) est la fonction tangente... Mais elle a toutes ses dérivées positives. Connaissez-vous une fonction dont seules les dérivées d'ordre pair sont positives ?
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 09 Mar 2012, 18:35
par Judoboy » 09 Mar 2012, 18:35
exp(-x) ?
Pas de message de moins de 10 caractères -.-
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités