Les suites et séries de fonctions

[Elerinna]

Voilà un exercice d'analyse sur les séries entières posé à un oral de l'X :

On définit la suite par :

et

a) Montrer que :

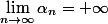
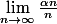
b) Determiner : . On pourra étudier

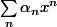
[SaintAmand]

Voilà un exercice d'analyse sur les séries entières posé à un oral de l'X :

Et alors ?

[Elerinna]

Et alors ?

Un retour aux réclammations de fonds publics d'aide à l'emploi et à la réinsertions des jeunes !

Actuellement en révision pour des concours, je cherche des exos d'oral de polytechnique. [...]

Personne n'interdit à quiconque de s'y pencher de près et d'ouvrir la boîte à outils d'amarrage.

[SaintAmand]

Un retour aux réclammations de fonds publics d'aide à l'emploi et à la réinsertions des jeunes !

Evidemment, suis-je bête...

[Le_chat]

Comment on fait pour montrer efficacement que la série entière a un rayon de convergence >0? J'ai utilisé le fait que (an) est plus petite que la suite de fibonnacci associée à a0,a1 mais c'est un peu lourd je pense.