Bonjour, je suis entrain de me confondre entre permutation et combinaison, objets discernables et indiscernables.
Par ex; si on a k=6 objets, et n=8 objet on veux savoir de combien de façon on peu les arranger.
Ok on fait 14!/(6!8!) , mais je n'arrive pas a comprendre si c'est discernables ou indiscernables.
Merci
Denombrement
5 messages
- Page 1 sur 1
Re: denombrement
bonjour,
soit un ensemble à n éléments
un ensemble à n éléments 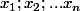
pour discerner les sous ensembles (les combinaisons)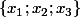 et
et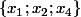 il faut bien que les éléments
il faut bien que les éléments 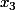 et
et 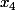 soient discernables
soient discernables
soit
pour discerner les sous ensembles (les combinaisons)
Re: denombrement
Ce que tu comptes avec le C ,
c'est du indiscernable.
par exemple si tu as k objets blancs et n objets noirs, tu cherches de combien de façon tu peux les ranger,
et bien tu cherches:
BBNBNNNBBN...
ou
NBNBBBNNB...
les blancs sont bien indiscernables, les noirs sont bien indiscernables
c'est ce que tu as fait avec ton C(14,6) qui est égal à ton C(14,8)
si on reprend ta formule
c'est du indiscernable.
par exemple si tu as k objets blancs et n objets noirs, tu cherches de combien de façon tu peux les ranger,
et bien tu cherches:
BBNBNNNBBN...
ou
NBNBBBNNB...
les blancs sont bien indiscernables, les noirs sont bien indiscernables
c'est ce que tu as fait avec ton C(14,6) qui est égal à ton C(14,8)
si on reprend ta formule
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: denombrement
c'est du discernable, on choisit des combinaisons d'indices des cases où l'on va mettre les boules noires
NNBNBBNN <---> {1;2;4;7;8}
NNBNBBNN <---> {1;2;4;7;8}
Re: denombrement
mathelot a écrit:c'est du discernable, on choisit des combinaisons d'indices des cases où l'on va mettre les boules noires
NNBNBBNN <---> {1;2;4;7;8}
Tout à fait d'accord.
mais tous les exos qui tirent des boules noires, rouges, truc
ben les boules sont indiscernables et dans l'exemple que j'ai pris ,
le C range les objets N et B de façon indiscernable (on ne discerne pas quel N , quel B,
et si ils devenaient discernables ces objets, alors ce ne serait plus le C mais le A que l'on utiliserait
"Ok on fait 14!/(6!8!) " c'est la formule du C(14,6) ou C(14,8), pas du A.
Mais ce serait bien que hsn détaille ce qu'il fait,
il cherche et calcule quoi.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
