Corps finis

par **jeancam** » 12 Déc 2008, 12:27

montere qu un corps fini est engendré par les elements d ordre premier.(je n ai pas dit d ordre une puissance de nombre premier)

par **abcd22** » 12 Déc 2008, 18:44

Bonjour,
C'est un exercice ou tu ne sais pas si c'est vrai ou pas ? Je pense que c'est faux : le groupe multiplicatif d'un corps fini est cyclique (plus généralement, tout sous-groupe fini du groupe multiplicatif d'un corps (commutatif) est cyclique), disons isomorphe à Z/nZ, avec

la décomposition en facteurs premiers de n. Par le théorème chinois, on a

. Comme un isomorphisme de groupes préserve l'ordre, les parties génératrices, etc., et que l'ordre d'un élément d'un groupe divise l'ordre du groupe, ce que tu veux revient à montrer que les éléments d'ordre p de

engendrent

pour tous p premier et a > 0.
Or pour tout entier m et tout diviseur d de m, l'ensemble des éléments x tels que dx = 0 (c'est-à-dire les éléments d'ordre divisant d) de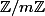

forme un sous-groupe de cardinal d (le sous-groupe {0, m/d, 2m/d, ... (d-1)m/d}).
Donc si a > 1, l'ensemble des éléments d'ordre p de

est inclus dans un sous-groupe strict donc ne forme pas une famille génératrice.
Pour résumer, ton résultat est vrai si et seulement si n = (cardinal du corps) - 1 est sans facteur carré.

par **jeancam** » 12 Déc 2008, 19:56

abcd22 a écrit:Bonjour,
C'est un exercice ou tu ne sais pas si c'est vrai ou pas ? Je pense que c'est faux : le groupe multiplicatif d'un corps fini est cyclique (plus généralement, tout sous-groupe fini du groupe multiplicatif d'un corps (commutatif) est cyclique), disons isomorphe à Z/nZ, avec la décomposition en facteurs premiers de n. Par le théorème chinois, on a . Comme un isomorphisme de groupes préserve l'ordre, les parties génératrices, etc., et que l'ordre d'un élément d'un groupe divise l'ordre du groupe, ce que tu veux revient à montrer que les éléments d'ordre p de engendrent pour tous p premier et a > 0.
Or pour tout entier m et tout diviseur d de m, l'ensemble des éléments x tels que dx = 0 (c'est-à-dire les éléments d'ordre divisant d) de forme un sous-groupe de cardinal d (le sous-groupe {0, m/d, 2m/d, ... (d-1)m/d}).
Donc si a > 1, l'ensemble des éléments d'ordre p de est inclus dans un sous-groupe strict donc ne forme pas une famille génératrice.
Pour résumer, ton résultat est vrai si et seulement si n = (cardinal du corps) - 1 est sans facteur carré.

pardon j ai dis groupe multiplicatif et c est justement faux je voulais dire le corps engendré. rectifié.merci

par **R.C.** » 12 Déc 2008, 20:12

Bonsoir,
j'ai comme l'impression que dans Fp^n, tous les éléments sont d'ordre p (pour l'addition).
C'est engendrent le corps en tant que corps ou en tant que groupe additif? Et c'est l'ordre additif ou multiplicatif?

par **jeancam** » 12 Déc 2008, 20:19

R.C. a écrit:Bonsoir,
j'ai comme l'impression que dans Fp^n, tous les éléments sont d'ordre p (pour l'addition).
C'est engendrent le corps en tant que corps ou en tant que groupe additif? Et c'est l'ordre additif ou multiplicatif?

les deux sont vrai. le cas non trivial est le cas multiplicatif comme tu l as souligné.

par **R.C.** » 12 Déc 2008, 20:25

J'ai comme l'impression que ca ne marche pas avec F9.

par **jeancam** » 12 Déc 2008, 20:53

R.C. a écrit:J'ai comme l'impression que ca ne marche pas avec F9.

en fait je crois l avoir démontré mais je me suis pas attardé sur le cas ou le cardinal du groupe multiplicatif est une puissance de deux...
oups...je crois que tu as raison!

par **jeancam** » 12 Déc 2008, 21:06

en fait çà revient à montrer que si j ai

pour n inferieur ou egal à m alors m=n.
sauf si p^m-1 est une puissance de 2 !!!

Corps finis

corps finis

Qui est en ligne