Continuité sans lever le crayon
63 messages
- Page 3 sur 4 - 1, 2, 3, 4
Re: Continuité sans lever le crayon
"Il se trouve que la définition mathématique de la "continuité" est la SEULE, à ma connaissance, qui n'a rien à voir avec notre schéma mental (notre intuition), "
Ben perso, la fonction f(x) = partie entière de x, je ne sais pas la tracer sans lever le crayon
il se trouve qu'elle n'est pas continue.J'en avais donné un autre exemple où idem je ne savais pas faire sans lever le crayon et c'était non continu.
des fonctions ax+b ou des paraboles pour prendre des fonctions simples connues,
ben je ne sais pas trouver un endroit de la courbe que je ne sais pas dessiner sans lever le crayon.
Je dirai sans rien y connaitre que ces fonctions m'ont l'air continues…
etc... donc le ressenti comme le dit Skullkid n'est pas le même pour tous.
Ben perso, la fonction f(x) = partie entière de x, je ne sais pas la tracer sans lever le crayon
il se trouve qu'elle n'est pas continue.J'en avais donné un autre exemple où idem je ne savais pas faire sans lever le crayon et c'était non continu.
des fonctions ax+b ou des paraboles pour prendre des fonctions simples connues,
ben je ne sais pas trouver un endroit de la courbe que je ne sais pas dessiner sans lever le crayon.
Je dirai sans rien y connaitre que ces fonctions m'ont l'air continues…
etc... donc le ressenti comme le dit Skullkid n'est pas le même pour tous.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Continuité sans lever le crayon
Le bémol que je mettrai aux explications de Ben314 c'est lorsqu'il dit:
"le premier truc qu'on (essaye) d'apprendre aux gamins, c'est que le graphe d'une fonction f, c'est pas n'importe quoi : à chaque x doit correspondre un unique y (ou "au plus un y si on accepte" de prendre des x qui sont pas dans Df) donc le graphe ne doit pas contenir de "retours en arrière" ni de "segments verticaux" alors que "sans lever le stylo", ben tu peut parfaitement faire des verticales ou des "retours en arrière". "
Si on parle de fonctions, on est d'abord une fonction
et ensuite celle-ci est continue ou non
donc le lever de stylo ne signifie ni retour arrière ni vertical puisque nous sommes dans le cadre d'une fonction
Si c'est la continuité d'autres notions OK la remarque a sans doute sa pertinence.
"le premier truc qu'on (essaye) d'apprendre aux gamins, c'est que le graphe d'une fonction f, c'est pas n'importe quoi : à chaque x doit correspondre un unique y (ou "au plus un y si on accepte" de prendre des x qui sont pas dans Df) donc le graphe ne doit pas contenir de "retours en arrière" ni de "segments verticaux" alors que "sans lever le stylo", ben tu peut parfaitement faire des verticales ou des "retours en arrière". "
Si on parle de fonctions, on est d'abord une fonction
et ensuite celle-ci est continue ou non
donc le lever de stylo ne signifie ni retour arrière ni vertical puisque nous sommes dans le cadre d'une fonction
Si c'est la continuité d'autres notions OK la remarque a sans doute sa pertinence.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Continuité sans lever le crayon
Pseuda a écrit:Je pars du principe que toutes les théories mathématiques partent d'une intuition, de notre schéma mental
Pourquoi pas, mais encore une fois le schéma mental de quelqu'un n'a aucune raison d'être le même que celui du voisin.
Pseuda a écrit:Il se trouve que la définition mathématique de la "continuité" est la SEULE, à ma connaissance, qui n'a rien à voir avec notre schéma mental (notre intuition), en tout cas la seule qui me pose problème. On a parlé ici d'événements indépendants, on peut parler de dérivée, d'intégration, de suites, de séries, de la fonction exponentielle, de variables aléatoires, ...., tout est conforme à notre schéma mental, ..., sauf la continuité. Je pense que ceci est difficile à nier.
Que la définition mathématique de continuité puisse avoir des facettes/conséquences contre-intuitives, je suis d'accord. Que toi, personnellement, tu les trouves "très" contre-intuitives, je ne peux évidemment pas le nier. Mais, parlant pour moi, partant de mes schémas mentaux, l'assertion "si X est une variable aléatoire uniforme sur [0,1], les événements (X = 0.1) et (X < 0.5) sont indépendants" me heurte bien davantage que "la fonction f définie par f(x) = x*sin(1/x) si x non nul et f(0) = 0 est continue sur [-1,1]". Je me souviens aussi avoir eu du mal à réconcilier certaines axiomatiques avec l'image mentale que j'étais censé m'en faire, typiquement les ouverts/fermés/voisinages en topologie. Ou pire, les ensembles ; je suis plutôt confiant qu'on a tous à peu près la même image mentale de ce qu'est un ensemble, mais manque de pot, le mot "ensemble" n'est jamais défini.
Pseuda a écrit:- il est impossible de définir la CSLC (attention une fonction qui vérifie le TVI n'est pas forcément continue et encore moins CSLC), en tout cas, personne n'y est jamais arrivé,
- une définition a été trouvée, mais elle n'a pas donné satisfaction pour ce qu'on voulait en faire,
Encore une fois, il y a une aporie fondamentale à parler de définition acceptable d'un concept sans donner les critères qui permettent de juger de cette acceptabilité. Pour l'instant le seul truc un peu concret que tu sembles attendre de la définition de CSLC c'est qu'elle exclue le cas x*sin(1/x), c'est un peu léger ! Autrement, ce que tu dis en substance c'est "je ne sais pas définir les fonctions CSLC, mais si j'en vois une je la reconnais tout de suite". Ça ne nous avance pas beaucoup...
Après ça n'empêche pas de continuer la discussion pour essayer de cerner un peu mieux le cahier des charges que devrait, selon toi, remplir une définition de CSLC.
Re: Continuité sans lever le crayon
Skullkid a écrit:Encore une fois, il y a une aporie fondamentale à parler de définition acceptable d'un concept sans donner les critères qui permettent de juger de cette acceptabilité.
Si tu veux un critère, le seul critère à mon sens est que tout le monde soit d'accord pour dire que la définition de la CSLC (laquelle ? à trouver, tout le problème est là) corresponde bien à notre ressenti, et qu'on puisse continuer notre chemin avec cette nouvelle définition, mais cela je n'en doute pas, car la CSLC est une condition plus forte (intuitivement) que la CM.
On parle de la fonction x*sin(1/x), mais il doit y avoir d'autres fonctions qui sont dans le même cas (à voir dans les sommes de séries...).
Par contre, l'assertion "les événements (X = 0.1) et (X < 0.5) sont indépendants" ne me choque pas : un événement impossible, ou bien certain, qui n'apporte pas d'information, est (intuitivement) indépendant de tous les événements.
En fait, pour aller au fond des choses, j'ai la nette impression (mais je peux me tromper totalement) que si on était arrivé à avoir une définition acceptable de la CSLC et qu'on l'avait adoptée, cela aurait simplifié l'analyse. Mais justement on n'y est pas arrivé. Pourquoi ?
Re: Continuité sans lever le crayon
Pseuda a écrit:Si tu veux un critère, le seul critère à mon sens est que tout le monde soit d'accord pour dire que la définition de la CSLC (laquelle ? à trouver, tout le problème est là) corresponde bien à notre ressenti
Toujours la même objection : le ressenti DE QUI ? Rien ne heurte mon ressenti dans la définition mathématique, donc je suis pas inclus dans ce "nous". Tant que tu te limites à ton ressenti ou au ressenti commun d'un certain groupe - lequel ? comment être sûr que tous ses membres ont bien le même ressenti ? - le seul moyen de savoir si une définition est "bonne" c'est de te demander. Tu vois bien que ça peut pas marcher...
Pour ce qui est de l'exemple avec les probas indépendantes, ça montre encore une fois que ton intuition n'est pas la mienne et que ça n'a aucune valeur opératoire de demander à une définition d'être "conforme à notre intuition".
Re: Continuité sans lever le crayon
soit le graphe de f , partie de  :
:
) / x \in \mathbb{R} \})
la définition mathématique de "continue sans lever le crayon"
est
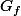 est connexe
est connexe
(ou/puis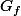 est connexe par arcs)
est connexe par arcs)
la définition mathématique de "continue sans lever le crayon"
est
(ou/puis
Re: Continuité sans lever le crayon
@mathelot Le problème, c'est que la définition de "connexe" (d'un seul tenant) est basée sur la continuité, donc on tourne en rond. Il faut une définition de CSLC qui n'utilise pas la définition de CM.
@Skullkid Finalement, je viens d'en parler avec un proche, c'est ce qui m'a le plus convaincue, et comme dit Beagle, le problème est exactement le même que celui entre 0,9999.... et 1. Mais tandis que j'accepte complétement que 0,9999...=1 (car par définition 0,999... est la limite de la série de TG 9*10^-n, et que par définition, cette limite c'est 1), je n'admets pas que la courbe de x*sin(1/x) soit au point 0 comme l'est la courbe de x^2.
Au point O, l'origine "touche" les points de la courbe de x^2, mais on a beau zoomer, elle ne "touche" jamais ceux de la courbe x*sin(1/x). D'où une différence, qui donne cette impression que la courbe x*sin(1/x) est considérée à tort comme continue.
Mais, et j'en resterai là, puisque mathématiquement il n'y a aucune différence, si on accepte que 0,999...=1, on doit accepter que la courbe de x*sin(1/x) est continue au point 0.
Merci à tous.
@Skullkid Finalement, je viens d'en parler avec un proche, c'est ce qui m'a le plus convaincue, et comme dit Beagle, le problème est exactement le même que celui entre 0,9999.... et 1. Mais tandis que j'accepte complétement que 0,9999...=1 (car par définition 0,999... est la limite de la série de TG 9*10^-n, et que par définition, cette limite c'est 1), je n'admets pas que la courbe de x*sin(1/x) soit au point 0 comme l'est la courbe de x^2.
Au point O, l'origine "touche" les points de la courbe de x^2, mais on a beau zoomer, elle ne "touche" jamais ceux de la courbe x*sin(1/x). D'où une différence, qui donne cette impression que la courbe x*sin(1/x) est considérée à tort comme continue.
Mais, et j'en resterai là, puisque mathématiquement il n'y a aucune différence, si on accepte que 0,999...=1, on doit accepter que la courbe de x*sin(1/x) est continue au point 0.
Merci à tous.
Re: Continuité sans lever le crayon
Bonjour,
A la lueur de mon dernier post, j'ai acquis maintenant la conviction que même si on trouvait une définition de la continuité "sans lever le crayon", elle serait presque équivalente à la définition mathématique de la continuité (*).
En fait, la confusion provient du fait que pour une courbe continue (sans ambiguïté comme x^2 au point O), le fait de "toucher" les points avoisinants sur la courbe, ne veut en fait rien dire. D'où la différence de traitement (avec la courbe x*sin(1/x) au point O) qui ne repose en fait sur rien.
La confusion vient du fait que pour la courbe x^2, 0 semble "toucher" les points avoisinants sur la courbe, tandis que c'est faux pour x*sin(1/x). Mais "toucher" ne veut rien dire, on peut seulement dire que la distance entre les points est très petite, aussi petite que l'on veut. Donc l'une et l'autre courbe répondent à la définition mathématique de la continuité, il n'y a aucune différence à ce niveau-là. La différence ne se situe pas là.
Désolée pour le dérangement (j'ai raconté pas mal de bêtises).
A la lueur de mon dernier post, j'ai acquis maintenant la conviction que même si on trouvait une définition de la continuité "sans lever le crayon", elle serait presque équivalente à la définition mathématique de la continuité (*).
En fait, la confusion provient du fait que pour une courbe continue (sans ambiguïté comme x^2 au point O), le fait de "toucher" les points avoisinants sur la courbe, ne veut en fait rien dire. D'où la différence de traitement (avec la courbe x*sin(1/x) au point O) qui ne repose en fait sur rien.
La confusion vient du fait que pour la courbe x^2, 0 semble "toucher" les points avoisinants sur la courbe, tandis que c'est faux pour x*sin(1/x). Mais "toucher" ne veut rien dire, on peut seulement dire que la distance entre les points est très petite, aussi petite que l'on veut. Donc l'une et l'autre courbe répondent à la définition mathématique de la continuité, il n'y a aucune différence à ce niveau-là. La différence ne se situe pas là.
Désolée pour le dérangement (j'ai raconté pas mal de bêtises).
Modifié en dernier par Pseuda le 13 Juin 2018, 12:26, modifié 1 fois.
Re: Continuité sans lever le crayon
(*) à ceci près que pour la continuité "sans lever le crayon", par exemple la fonction x^2, cette fonction est monotone dans un voisinage à droite et monotone dans un voisinage à gauche de 0, ce que ne vérifie pas la fonction x*sin(1/x) ; mais ceci doit expliquer pourquoi l'une est dérivable à droite et à gauche (explication à vérifier : monotone à droite => dérivable à droite au sens large :+/- infini accepté) et l'autre ne l'est pas.
La continuité "sans lever le crayon" serait la continuité au sens mathématique + la monotonie dans une direction et un sens.
La continuité "sans lever le crayon" serait la continuité au sens mathématique + la monotonie dans une direction et un sens.
Re: Continuité sans lever le crayon
Bonsoir !
Je ne comprends pas ton dernier message.
En prenant la fonction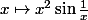 avec le prolongement usuel tu as la dcontinuité ET la dérivabilité mais aucune monotonie locale.
avec le prolongement usuel tu as la dcontinuité ET la dérivabilité mais aucune monotonie locale.
...................................
Je profite de ce passage pour donner une suggestion concernant le dessin du 15-10-2017 où quelqu'un demandait le libellé de la fonction.
Je ne peux donner ce libellé mais des indications permettant d'obtenir une courbe analogue.
En espérant ne pas laisser d'erreurs...
On peut facilement obtenir des dessins de ce type en prenant la fonction) (distance d'un point à un ensemble) où
(distance d'un point à un ensemble) où  est l'ensemble des images d'une suite
est l'ensemble des images d'une suite 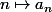 strictement décroissante de limite
strictement décroissante de limite  .
.
En réunissant à les opposés de ces termes on a même un dessin symétrique par rapport à l'axe des ordonnées.
les opposés de ces termes on a même un dessin symétrique par rapport à l'axe des ordonnées.
On justifie facilement que le graphe, entre deux points consécutifs de la suite, est formé par les côtés d'un triangle rectangle isocèle d’hypoténuse joignant les points,\;(a_n,0)) .
.
On peut justifier aussi que le coefficient directeur de la droite joignant l'origine à un point de la courbe oscille entre et
et 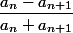 .
.
Avec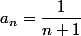 la suite majorante de ces coefficients directeurs a une limite nulle donc la dérivée en
la suite majorante de ces coefficients directeurs a une limite nulle donc la dérivée en  existe et vaut
existe et vaut  .
.
En revanche avec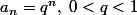 l'oscillation se fait entre les valeurs constantes
l'oscillation se fait entre les valeurs constantes 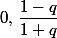 : la fonction n'est alors pas dérivable en
: la fonction n'est alors pas dérivable en  .
.
Je ne comprends pas ton dernier message.
En prenant la fonction
...................................
Je profite de ce passage pour donner une suggestion concernant le dessin du 15-10-2017 où quelqu'un demandait le libellé de la fonction.
Je ne peux donner ce libellé mais des indications permettant d'obtenir une courbe analogue.
En espérant ne pas laisser d'erreurs...
On peut facilement obtenir des dessins de ce type en prenant la fonction
En réunissant à
On justifie facilement que le graphe, entre deux points consécutifs de la suite, est formé par les côtés d'un triangle rectangle isocèle d’hypoténuse joignant les points
On peut justifier aussi que le coefficient directeur de la droite joignant l'origine à un point de la courbe oscille entre
Avec
En revanche avec
Re: Continuité sans lever le crayon
Kolis a écrit:Bonsoir !
Je ne comprends pas ton dernier message.
En prenant la fonctionavec le prolongement usuel tu as la continuité ET la dérivabilité mais aucune monotonie locale.
Bonsoir,
Je ne vois pas la contradiction. La fonction
Oui bon, la dérivabilité n'aurait rien à voir là-dedans : dérivable n'implique pas "sans lever le crayon". Ce qui compterait, ce serait : continuité mathématique + monotonie dans un voisinage à droite (à gauche) pour être continue sans lever le crayon à droite (à gauche).
Re: Continuité sans lever le crayon
Bonjour,
Pour conclure (parce qu'il le faut bien), "continue sans lever le crayon" serait :
- en un point :
continue sans lever le crayon à droite (à gauche) = continuité mathématique à droite (à gauche) + monotonie dans un voisinage à droite (à gauche) ;
continue sans lever le crayon en un point = continue sans lever le crayon à droite (et définie à droite) et sans lever le crayon à gauche (et définie à gauche).
- sur un intervalle : continue sans lever le crayon sur tous les points de l'intervalle.
J'espérais une définition directement sur un intervalle, mais bon. Cette définition peut être remise en cause par une fonction qui la vérifierait et qui ne serait pas (dans notre schéma mental) continue sans lever le crayon, ou inversement qui ne la vérifierait pas et qui serait (dans notre schéma mental) continue sans lever le crayon.
Pour conclure (parce qu'il le faut bien), "continue sans lever le crayon" serait :
- en un point :
continue sans lever le crayon à droite (à gauche) = continuité mathématique à droite (à gauche) + monotonie dans un voisinage à droite (à gauche) ;
continue sans lever le crayon en un point = continue sans lever le crayon à droite (et définie à droite) et sans lever le crayon à gauche (et définie à gauche).
- sur un intervalle : continue sans lever le crayon sur tous les points de l'intervalle.
J'espérais une définition directement sur un intervalle, mais bon. Cette définition peut être remise en cause par une fonction qui la vérifierait et qui ne serait pas (dans notre schéma mental) continue sans lever le crayon, ou inversement qui ne la vérifierait pas et qui serait (dans notre schéma mental) continue sans lever le crayon.
Re: Continuité sans lever le crayon
Bonsoir,
J'en reviens au point de départ : avec cette définition (donnée dans mon message précédent) de "fonction continue sans lever le crayon", est-ce qu'une fonction qui serait continue "sans lever le crayon" et dérivable sur un intervalle, serait toujours de dérivée continue sur cet intervalle ?
J'ai l'impression que oui (car cela élimine les cas tordus, comme x^2*sin(1/x), mais il y a peut-être des cas encore plus tordus qui m'échappent).
Démonstration ou contre-exemple ?
J'en reviens au point de départ : avec cette définition (donnée dans mon message précédent) de "fonction continue sans lever le crayon", est-ce qu'une fonction qui serait continue "sans lever le crayon" et dérivable sur un intervalle, serait toujours de dérivée continue sur cet intervalle ?
J'ai l'impression que oui (car cela élimine les cas tordus, comme x^2*sin(1/x), mais il y a peut-être des cas encore plus tordus qui m'échappent).
Démonstration ou contre-exemple ?
Re: Continuité sans lever le crayon
en série ES, on a pas les quantificateurs, continue est défini par 'sans lever le crayon', et ça suffit largement pour interpréter les courbes.
Dérivable est toujours C1 en fait car on doit pouvoir appliquer le TVI sans faire toute la théorie derrière. Perso j'ai toujours au moins expliqué la différence entre monotone et strictement monotone pour l'unicité dans le tvi, on peut l'expliquer... sans lever le crayon.
Pour des fonction bizarres : je pense qu'on va ensuite taper dans les familles de fonction avec convergence simple, des constructions itératives (fractale) ou jouer sur des points isolés où la fonction n'est pas dérivable te faire se rapprocher ses points, des ensembles denses dans R.
Dérivable est toujours C1 en fait car on doit pouvoir appliquer le TVI sans faire toute la théorie derrière. Perso j'ai toujours au moins expliqué la différence entre monotone et strictement monotone pour l'unicité dans le tvi, on peut l'expliquer... sans lever le crayon.
Pour des fonction bizarres : je pense qu'on va ensuite taper dans les familles de fonction avec convergence simple, des constructions itératives (fractale) ou jouer sur des points isolés où la fonction n'est pas dérivable te faire se rapprocher ses points, des ensembles denses dans R.
Re: Continuité sans lever le crayon
un exemple de fonction continue sur  et nulle part dérivable
et nulle part dérivable
=\Sum_{n=0}^{+\infty} \, (\frac{2}{3})^n \, sin((\frac{5}{2})^n \, x))
Cauchy professait à l'X que les fonctions continues étaient dérivables jusqu'à ce que Weierstrass
exhibe ce contre exemple
Cauchy professait à l'X que les fonctions continues étaient dérivables jusqu'à ce que Weierstrass
exhibe ce contre exemple
Re: Continuité sans lever le crayon
peut-on la tracer sans lever le crayon(et avec un seul trait, sans noircir toute une zone) ?
Re: Continuité sans lever le crayon
non, on ne peut pas tracer sa courbe sans "lever le crayon" 
d'ailleurs, on ne peut pas tracer sa courbe même en levant le crayon - à confirmer-
d'ailleurs, on ne peut pas tracer sa courbe même en levant le crayon - à confirmer-
Re: Continuité sans lever le crayon
Ca doit donner une zone grise plus ou moins dense
Pour la continuité sans lever le crayon :
Au crayon, je ne voit pas comment on peut faire autrement qu'une fonction avec un nombre fini de points où la fonction est continue non dérivable. Mais avec la notion de fractale, on peut dire qu'à toute les échelles, elle est comme ça et bien avoir une fonction traçable à une échelle mais dont on ne peut pas voir tous les problèmes (en nombre infini et dénombrables, on se rapproche).
Pour la continuité sans lever le crayon :
Au crayon, je ne voit pas comment on peut faire autrement qu'une fonction avec un nombre fini de points où la fonction est continue non dérivable. Mais avec la notion de fractale, on peut dire qu'à toute les échelles, elle est comme ça et bien avoir une fonction traçable à une échelle mais dont on ne peut pas voir tous les problèmes (en nombre infini et dénombrables, on se rapproche).
Re: Continuité sans lever le crayon
mathelot a écrit:un exemple de fonction continue suret nulle part dérivable
Cauchy professait à l'X que les fonctions continues étaient dérivables jusqu'à ce que Weierstrass
exhibe ce contre exemple
Bonjour,
Es-tu sûr de cela ? La fonction valeur absolue est visiblement continue sur R, non dérivable en 0. Ce ne serait pas : les fonctions continues et dérivables sont de dérivée continue (qui était enseigné par Cauchy à l'X) ? Merci quand même pour l'exemple. La somme de la série (qui converge uniformément sur R) est une fonction continue. La somme dérivée ne paraît pas converger, même pas simplement : donc dérivable nulle part ?
mathelot a écrit:non, on ne peut pas tracer sa courbe sans "lever le crayon"
d'ailleurs, on ne peut pas tracer sa courbe même en levant le crayon - à confirmer-
En effet, on ne peut pas la tracer du tout (sauf si elle converge vers une fonction simple, mais je n'ai pas l'impression, sinon elle serait dérivable) , en levant le crayon ou non. Parmi les fonctions qu'on ne peut pas tracer sans lever le crayon, il y a les fonctions qu'on ne peut pas tracer du tout, et celles qu'on peut tracer en levant le crayon (fonctions continues au sens "sans lever le crayon" par morceaux).
pascal16 a écrit:Dérivable est toujours C1 en fait car on doit pouvoir appliquer le TVI sans faire toute la théorie derrière. Perso j'ai toujours au moins expliqué la différence entre monotone et strictement monotone pour l'unicité dans le tvi, on peut l'expliquer... sans lever le crayon.
Le TVI s'applique à une fonction continue, fonction C1 ou dérivable n'a rien à voir là-dedans ?
Merci à tous deux pour vos réponses, mais elles ne paraissent pas répondre à la question posée. La question est (pour faire simple) : une fonction continue, monotone, et dérivable sur un intervalle est-elle toujours de dérivée continue (de classe C1) sur cet intervalle ? Graphiquement, la réponse paraît oui.
Re: Continuité sans lever le crayon
Pseuda a écrit:: une fonction continue, monotone, et dérivable sur un intervalle est-elle toujours de dérivée continue (de classe C1) sur cet intervalle ? Graphiquement, la réponse paraît oui.
Salut,
Je ne sais pas si cela a été évoqué, mais si une fonction f de R dans R par exemple est dérivable, alors le théorème de Baire permet de démontrer que l'ensemble des points de continuité de f' est dense dans R.
Je ne sais pas si cela apporte un élément de réponse à ta question?
Si en plus on ajoute que f est monotone...
Je me souviens d'un autre résultat qui indiquait que l'ensemble des points de discontinuité de f devenait alors au plus dénombrable.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
63 messages
- Page 3 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
