Chainette passant par 2 points de hauteur différentes

[ssouron]

Bonjour à tous.

Je n'ai pas le niveau requis pour résoudre un problème, aussi je demande de l'aide. Lors de l'installation de câbles entre deux poteaux, de hauteurs qui peuvent être différentes, je dois pouvoir être en mesure de donner la hauteur du point le plus bas du câble.
Après de longues recherches de documentation, j'ai trouvé une page très intéressante sur la courbe de chainette (qui est la forme que prend le câble), à cette adresse :
http://serge.mehl.free.fr/anx/catena.html .

L'auteur de cette page aborde à un moment le problème général où la courbe passe par deux points, mais sans le développer. J'ai bien essayé de suivre la piste qu'il donne, mais sans succès.

J'aimerais pouvoir obtenir la hauteur du point le plus bas du câble en fonction de :
- la hauteur de chacun des points d'accrochage
- la distance entre les deux points d'accrochage
- la longueur du câble à suspendre
- la masse linéique du câble

Si en plus je suis capable d'exprimer, en fonction de ces paramètres, la force de traction exercée sur chacun des poteaux, alors ce serait byzance !


Merci d'avance à ceux qui auront l'amabilité de bien vouloir passer un peu de temps sur ce problème, je suis loin d'avoir le niveau requis...

[Ben314]

Un premier élément de réponse :
La courbe est toujours un cosinus hyperbolique et, sauf erreur la forme ne dépend pas de la masse linéique du câble (à condition de le supposer suffisement souple....)
Ensuite, je n'ai pas encore écrit les équations, mais je ne suis pas sur que l'on puisse exprimer h=fonction_élémentaires_des_autres_variables.
On risque de pouvoir seulement écrire "h est LA solution de l'équation ..." ce qui permet d'en calculer des valeurs approchées aussi précise que l'on veut.

Je regarde ça d'ici une petite heure (j'ai pas encore mangé...)

[ssouron]

Je me doute bien qu'il ne sera pas possible de donner une raltion simple du type h=f(ceci / cela)... Quant à la masse linéique, elle sera par contre indispensable pour calculer les composantes verticales et horizontales de tractions sur les points d'accroche.

Merci d'avance et bon appétit, il n'y a aucune urgence !

[Ben314]

On note H1, H2 les deux hauteurs, D la distance entre les deux poteaux et L la longueur du cable.
L'équation cherchée est de la forme (dans le repère centré au pied du premier poteau) où a,b,k sont des constantes à déterminer. On a donc les trois équations :
(premier poteau x=0, y=H1)
(deuxième poteau x=D, y=H2)
(longueur du cable)
Ce qui donne et les 2 équations (c.f. trigo hyperbolique...) :


d'où, comme , on a :
c'est à dire

On ne sait pas "résoudre formellement" cette équation, mais, connaissant L,H1,H2 et D et sachant que la fonction est croissante sur on peut approximer (par exemple par dichotomie) l'unique solution : cela donne la valeur de donc celle de puis on déduit d'une des 2 équations au dessus celle de et de la première équation celle de (j'espère ne pas m'être trompé dans les calculs...)

La fonction a comme valeur minimale pour 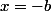qui est bien situé entre les deux poteaux.... si (sinon, le point le plus bas est un des deux poteaux).

Pour les forces, j'ai un peu la flemme d'écrire les calculs : tu écrits qu'au deux poteaux les forces sont dirigées dans l'axe des cables donc qu'elles sont respectivement égales à et où tu détermine et en disant que la somme des 2 force plus la force d'attraction (0,-mg) doit être nulle (où m=L*masse_linéique est la masse totale du cable)

....ouf....

P.S. Si tu trouve des valeurs absurdes, c'est que... je me suis gourré....