Arithmétique
19 messages
- Page 1 sur 1
Arithmétique
Soit n un entier relatif
Montrer que le produit (n-2)(n-1)n(n+1)(n+2) est un multiple de 5
Merci d'avance :lol3:
Montrer que le produit (n-2)(n-1)n(n+1)(n+2) est un multiple de 5
Merci d'avance :lol3:
Monsieur23 a écrit:Aloha,
Ou alors, par théorème des trous de pigeons (pigeonhole principle), parmi 5 nombres consécutifs, il y en a forcément un qui est un multiple de 5, et donc leur produit aussi.
C'est pour la première fois que j'entend parler de ce Théorème Monsieur23. J'aimerais voir comment tu l'appliques dans cet excercise. Merci
salut
si n = 5q + r avec 0 =< r < 5 est la division euclidienne d n par 5 alors
n - 2, n - 1, n, n + 1 et n + 2 sont 5q + r - 2, 5q + r - 1, 5q + r, 5q + r + 1 et 5q + r + 2
l'un des nombres r - 2, r - 1, r, r + 1, r + 2 avec 0 =< r < 5 est 0 ou 5 ....
si n = 5q + r avec 0 =< r < 5 est la division euclidienne d n par 5 alors
n - 2, n - 1, n, n + 1 et n + 2 sont 5q + r - 2, 5q + r - 1, 5q + r, 5q + r + 1 et 5q + r + 2
l'un des nombres r - 2, r - 1, r, r + 1, r + 2 avec 0 =< r < 5 est 0 ou 5 ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:salut
si n = 5q + r avec 0 =< r < 5 est la division euclidienne d n par 5 alors
n - 2, n - 1, n, n + 1 et n + 2 sont 5q + r - 2, 5q + r - 1, 5q + r, 5q + r + 1 et 5q + r + 2
l'un des nombres r - 2, r - 1, r, r + 1, r + 2 avec 0 =< r < 5 est 0 ou 5 ....
C'est un peu dur à cerner
Est-ce le théorème des trous de pigeons? Si oui, j'aimerais avoir l'énoncé de ce théorème car je ne suis pas sûr de le connaître. Merci
Sherlock Cainfri a écrit:C'est un peu dur à cerner
Est-ce le théorème des trous de pigeons? Si oui, j'aimerais avoir l'énoncé de ce théorème car je ne suis pas sûr de le connaître. Merci
Théorème des trou de pigeons est une traduction de l'anglais "pigeon whole" mal adapter, en français il est plus
connu sous le nom de principe des tiroir : n tiroir, n+1 balle -> un tiroir avec au moins deux balle ^^
c'est vrai que je ne vois pas où le principe des tiroir est utiliser ici, mais la méthode proposer par zygomatique
est beaucoup plus élémentaire et simple que le bulldozer proposer par mathelot ^^
c'est pourtant simple :
si n est un multiple de 5 alors c'est gagné,
si n = 5k+1 alors n-1 est un multiple de 5, c'est fini.
si n=5k+2, alors n-2 est un multiple de 5 : fini
si n=5k+3, alors n+2 est un multiple de 5 : fini
si n=5k+4 alors n+1 est un multiple de 5 Qed.
je trouve que comme ça on comprend bcp mieux pourquoi le produit est divisible par 5 que dire
hop petit théorème de Fermat, formule magique : c'est divisible par 5 cool :zen:
:lol3:
bolza a écrit:Théorème des trou de pigeons est une traduction de l'anglais "pigeon whole" mal adapter, en français il est plus
connu sous le nom de principe des tiroir : n tiroir, n+1 balle -> un tiroir avec au moins deux balle ^^
c'est vrai que je ne vois pas où le principe des tiroir est utiliser ici, mais la méthode proposer par zygomatique
est beaucoup plus élémentaire et simple que le bulldozer proposer par mathelot ^^
c'est pourtant simple :
si n est un multiple de 5 alors c'est gagné,
si n = 5k+1 alors n-1 est un multiple de 5, c'est fini.
si n=5k+2, alors n-2 est un multiple de 5 : fini
si n=5k+3, alors n+2 est un multiple de 5 : fini
si n=5k+4 alors n+1 est un multiple de 5 Qed.
je trouve que comme ça on comprend bcp mieux pourquoi le produit est divisible par 5 que dire
hop petit théorème de Fermat, formule magique : c'est divisible par 5 cool :zen:
:lol3:
Expliqué comme ca c'est beaucoup plus simple à comprendre :ptdr:
N'empêche que en devoir le petit théorème de Fermat va te faire gagner du temps
Merci bien Bolza
Sherlock Cainfri a écrit:Expliqué comme ca c'est beaucoup plus simple à comprendre :ptdr:
N'empêche que en devoir le petit théorème de Fermat va te faire gagner du temps
Merci bien Bolza
Fermat pour démontrer ce truc c'est vraiment une honte, non?
A l'école primaire on apprend les tables de multiplication, et on entoure les multiples sur la ligne numérique, les multiples de 5 arrivent assez régulièrement, c'est comme si ils arrivaient tous les 5 , de 5 en 5,dingue non?
bref le modulo c'est la classe OK,
n'empèche qu'entre 5k et 5(k+1) on ne trouvera jamais plus de 4 consécutifs non multiples de 5.
On retombe sur le modulo mais ce sont 5k+1, 5k+2, 5k+3, 5k+4.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
beagle a écrit:Fermat pour démontrer ce truc c'est vraiment une honte, non?
A l'école primaire on apprend les tables de multiplication, et on entoure les multiples sur la ligne numérique, les multiples de 5 arrivent assez régulièrement, c'est comme si ils arrivaient tous les 5 , de 5 en 5,dingue non?
bref le modulo c'est la classe OK,
n'empèche qu'entre 5k et 5(k+1) on ne trouvera jamais plus de 4 consécutifs non multiples de 5.
On retombe sur le modulo mais ce sont 5k+1, 5k+2, 5k+3, 5k+4.
Hahaha... Je comprend ce que tu dis Bealge... Utiliser la méthode des multiples de 5 donne une compréhension totale et paraît évident...
Mais utiliser le petit théorème de Fermat est loin d'être une honte et à mon humble avis cela prouve que tu fais bon usage de tes outils Mathématiques car une chose est de connaître mais l'autre chose est de savoir comment utiliser. De plus, lorsque tu a une épreuve de maths kilométrique et que tu ne viens pas vite sur la méthode des multiples de 5, le petit théorème de Fermat me paraît être un bon échappatoir pour te faire gagner du temps :we:
ouais enfin ... les multiples de 5 sont appris dès la primaire ...
ou encore :: dans une division par n il n'y a que n reste distincts ... (cours de 3e : division euclidienne)
donc n - 2, n - 1, n, n + 1 et n + 2 donnent 5 reste distincts .... donc l'un est 0 ...
c'est comme utiliser la dérivée pour étudier les variations de la fonction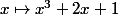 qui est simplement somme de deux fonctions croissantes dont croissante ....
qui est simplement somme de deux fonctions croissantes dont croissante ....
:zen:
ou encore :: dans une division par n il n'y a que n reste distincts ... (cours de 3e : division euclidienne)
donc n - 2, n - 1, n, n + 1 et n + 2 donnent 5 reste distincts .... donc l'un est 0 ...
c'est comme utiliser la dérivée pour étudier les variations de la fonction
:zen:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Oui, tu as raison. Peut être que cet exercice est simple et mérite un raisonnement plus simple, claire et compréhensible par tous pour être résolu.
Mais quand tu dis que >, je te répond que rien n'a été affirmé sans preuve. Car les deux méthodes aboutissent au même résultat et ont toutes deux des bases solides (on sait tous que le petit théorème de Fermat se démontre clairement). De plus ce théorème est tout aussi utile que le théorème de Pithagore ou tout autre théorème qu'on ne se gêne d'utiliser (sachant que chacun est libre d'utiliser la méthode qui lui convient).
Mais quand tu dis que >, je te répond que rien n'a été affirmé sans preuve. Car les deux méthodes aboutissent au même résultat et ont toutes deux des bases solides (on sait tous que le petit théorème de Fermat se démontre clairement). De plus ce théorème est tout aussi utile que le théorème de Pithagore ou tout autre théorème qu'on ne se gêne d'utiliser (sachant que chacun est libre d'utiliser la méthode qui lui convient).
la citation qui est ma signature n'a rien à voir avec ta démonstration ....
si tu veux utiliser une pelleteuse pour creuser un trous de 1000 cm^3 tu as le droit ....
pour ma part une pelle me suffit amplement ... et me donne l'occasion de faire de l'exercice physique ....
:zen:
si tu veux utiliser une pelleteuse pour creuser un trous de 1000 cm^3 tu as le droit ....
pour ma part une pelle me suffit amplement ... et me donne l'occasion de faire de l'exercice physique ....
:zen:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:la citation qui est ma signature n'a rien à voir avec ta démonstration ....
si tu veux utiliser une pelleteuse pour creuser un trous de 1000 cm^3 tu as le droit ....
pour ma part une pelle me suffit amplement ... et me donne l'occasion de faire de l'exercice physique ....
:zen:
My mistake :ptdr:
Au risque d'en rajouter une couche ...,
Là tu as de la chance, tu as le produit de 5 nombres consécutifs et 5 est premier,
mais si à l'examen on te ressort le même exercice, mais avec le produit de 6 nombres consécutifs
tu sera bien embêter avec ton théorème de Fermat.
De plus tu avances la rapidité de la méthode, mais est tu certain qu'elle est plus rapide ?
là mathelot t'a mâché le travail, il t'a directement donner le polynôme, mais développer
(n-2)(n-1)n(n+1)(n+2) à la main, ça prend quand même un certain temps.
Si à l'examen au lieu de 5 tu as 7 nombre consécutif, je te souhaite bien du courage pour
développer le polynôme (bien qu' avec une petite astuce tu puisses gagner quelques étapes).
De plus, faire le développement à la main peut être une source d'erreur.
Si dans ton développement tu fais une erreur de calcul, eh bien ton exercice que tu aurais pu
résoudre en quelque minute, peut finir par te prendre une demi-heure.
Mais bon, après effectivement tu es libre d'appliquer la méthode de ton choix.
Encore que pour être complètement correcte, il faudrait que tu t'assure qu'il existe une preuve du
petit théorème de Fermat qui n'utilise nulle part le résultat que tu veux démontrer.....
Là tu as de la chance, tu as le produit de 5 nombres consécutifs et 5 est premier,
mais si à l'examen on te ressort le même exercice, mais avec le produit de 6 nombres consécutifs
tu sera bien embêter avec ton théorème de Fermat.
De plus tu avances la rapidité de la méthode, mais est tu certain qu'elle est plus rapide ?
là mathelot t'a mâché le travail, il t'a directement donner le polynôme, mais développer
(n-2)(n-1)n(n+1)(n+2) à la main, ça prend quand même un certain temps.
Si à l'examen au lieu de 5 tu as 7 nombre consécutif, je te souhaite bien du courage pour
développer le polynôme (bien qu' avec une petite astuce tu puisses gagner quelques étapes).
De plus, faire le développement à la main peut être une source d'erreur.
Si dans ton développement tu fais une erreur de calcul, eh bien ton exercice que tu aurais pu
résoudre en quelque minute, peut finir par te prendre une demi-heure.
Mais bon, après effectivement tu es libre d'appliquer la méthode de ton choix.
Encore que pour être complètement correcte, il faudrait que tu t'assure qu'il existe une preuve du
petit théorème de Fermat qui n'utilise nulle part le résultat que tu veux démontrer.....
bolza a écrit:Théorème des trou de pigeons est une traduction de l'anglais "pigeon whole" mal adapter, en français il est plus
connu sous le nom de principe des tiroir : n tiroir, n+1 balle -> un tiroir avec au moins deux balle ^^
c'est vrai que je ne vois pas où le principe des tiroir est utiliser ici
Je t'avoue qu'en relisant, j'vois pas non plus
« Je ne suis pas un numéro, je suis un homme libre ! »
théorème des trous de pigeons est une traduction de l'anglais "pigeon whole" mal adapter, en français il est plus connu sous le nom de principe des tiroirs : n tiroirs, n+1 balles
attention à ne pas supprimer ce qui est aligné ... :ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
