Trouver l'équation de cette fonction

[upium666]

Bonjour à tous !
Ceci est un petit exercice que j'ai créé moi-même, je connais la solution mais je me suis dit que ça aurait été sympathique de le partager avec vous

On vous demande de trouver l'équation de cette fonction :
En fait, c'est une simple fonction sinusoïdale
Je vous "aide" (même si vous n'en avec pas réellement besoin) :
f(x)=;)*sin(x)

En bref, trouvez de telle manière qu'on n'obtienne qu'une seule "vague" complète de la fonction sin(x)

Bon casse-tête !

[John Philip C. Manson]

Bonjour à tous !
Ceci est un petit exercice que j'ai créé moi-même, je connais la solution mais je me suis dit que ça aurait été sympathique de le partager avec vous

On vous demande de trouver l'équation de cette fonction :
En fait, c'est une simple fonction sinusoïdale
Je vous "aide" (même si vous n'en avec pas réellement besoin) :
f(x)=;)*sin(x)

En bref, trouvez de telle manière qu'on n'obtienne qu'une seule "vague" complète de la fonction sin(x)

Bon casse-tête !

Quand tu parles d'une «vague» complète de la fonction, cela est-il équivalent à un sinusoïde situé strictement au-dessus de l'axe des abscisses ? Ou bien cela veut-il dire autre chose ?


En examinant l'image du graphique, pour que a×sin(pi/2) = 1 et pour que a×sin(pi) = a×sin 0 = 0, alors a = 1.

Justification : a = 1 / arcsin (pi/2) = 1 / arcsin (pi) = 1

[upium666]

Quand tu parles d'une «vague» complète de la fonction, cela est-il équivalent à un sinusoïde situé strictement au-dessus de l'axe des abscisses ? Ou bien cela veut-il dire autre chose ?

Cela veut tout simplement dire la fonction que tu vois (je t'avance pas à grand chose je sais)
Remarque que le domaine de définition est [0;2*pi]
Tu ne peux donc pas avoir a=1 comme solution !

[Nightmare]

Pourquoi la fonction définie sur [0;2pi] ne conviendrait-elle pas?

[Skullkid]

Bonjour, en fait si je comprends bien, ce que tu as en tête pour ton a c'est une expression algébrique de x qui ne soit définie que sur [0,2pi] est qui soit constamment égale à 1 sur cet intervalle, du genre (sauf que celle-ci n'est définie que sur ]0,2pi[)...

Ça vient probablement du fait que tu n'as jamais rencontré que des fonctions données sous la forme f(x) = machin, définies sur le plus gros sous-ensemble de R pour lequel l'expression f(x) a un sens. Mais ce n'est pas la seule manière de définir des fonctions. Il est par exemple tout à fait permis de parler de "la fonction définie par f(x) = 2x si et seulement si x est inférieur à 5 et f(x) = 8x-4 si et seulement si x est compris entre 8 et 10". Cette fonction n'est définie que sur ]-l'infini,5] union [8,10], même si les expressions algébriques 2x et 8x-4 ont un sens pour tous les nombres réels x. D'où la réponse de Nightmare, qui est la plus simple et la plus naturelle.

[upium666]

Pourquoi la fonction définie sur [0;2pi] ne conviendrait-elle pas?

Elle conviendrait mais le petit plus dans cet exercice est de ne pas ajouter de détails par une phrase du genre "avec x compris entre 0 et 2*pi".
En bref, je ne demande qu'un :
f(x)=???
Point.

[Sylviel]

En fait pour définir une fonction il faut donner son domaine de définition et son ensemble d'arrivée... Du coup je ne vois pas trop ce que tu cherches à nous faire dire.

[newman]

voici un exemple pour que tu comprennes upium666: la fonction indicatrice

[url]http://fr.wikipedia.org/wiki/Fonction_caractéristique_(théorie_des_ensembles)[/url])

[Judoboy]

Elle conviendrait mais le petit plus dans cet exercice est de ne pas ajouter de détails par une phrase du genre "avec x compris entre 0 et 2*pi".
En bref, je ne demande qu'un :
f(x)=???
Point.

No offense mais c'est idiot comme question. Si vraiment tu y tiens on peut multiplier par un truc comme ln(x)/ln(x) pour que ça soit pas défini pour x<0 mais ça a vraiment aucun intérêt. Lis le message de Skullkid plutôt.

[John Philip C. Manson]

La fonction représentée sous forme graphique dans l'image correspond à f(x) = sin x. La forme a×sin x implique que a = 1.

Si 'a' était différent de 1, les maximums de la courbe ne seraient pas à la hauteur f(x) = 1 ou -1, mais à la valeur 'a'.

Je ne comprends pas la question. Je suis cependant sûr que a = 1 étant donné l'image du graphique.

[Judoboy]

La fonction représentée sous forme graphique dans l'image correspond à f(x) = sin x. La forme a×sin x implique que a = 1.

Si 'a' était différent de 1, les maximums de la courbe ne seraient pas à la hauteur f(x) = 1 ou -1, mais à la valeur 'a'.

Je ne comprends pas la question. Je suis cependant sûr que a = 1 étant donné l'image du graphique.

La question porte sur le domaine de définition plus que sur la valeur numérique de a, si j'ai bien compris.

[Nightmare]

Et à mon avis, dans la tête de l'auteur, a se voulait être une fonction non nécessairement constante.

[John Philip C. Manson]

f(x) = a×sin x

je peux aussi dire que c'est égal à (a×i/2)(e^(-ix) - e^(ix))


Mais réfléchissons : si 'a' n'est pas constante et qu'elle est elle-même une fonction, alors la courbe dans l'image ne devrait pas être rigoureusement régulière.

Puis aussi, quelque soit le domaine de définition de la courbe de l'image, le coefficient vaut toujours a=1.

Supposons par exemple que a = ln x, alors f(x) = ln x × sin x, et la partie réelle de la courbe est explicitement irrégulière, voir ici : http://www.wolframalpha.com/input/?i=y+%3D+%28ln+x%29+*sin+x Même remarque avec une autre fonction, du genre f(x) = (x² - x - 1) × sin x : http://www.wolframalpha.com/input/?i=y+%3D+%28x%C2%B2-x-1%29+*sin+x

Je pense qu'une courbe régulière (comme celle de l'image), avec les mêmes maximums, implique un coefficient constant.

[manoa]

pourquoi pas :



http://www.wolframalpha.com/input/?i=y+%3D+2%28sqrt%7Bx%282pi-x%29%7D%2F%28sqrt%283%29pi%29+*sin+x

ce n'est bien sûr pas le sin mais elle a les mêmes extremums, sinon je vois pas trop aussi ..

[chan79]

Bonjour à tous !
Ceci est un petit exercice que j'ai créé moi-même, je connais la solution mais je me suis dit que ça aurait été sympathique de le partager avec vous

On vous demande de trouver l'équation de cette fonction :
En fait, c'est une simple fonction sinusoïdale
Je vous "aide" (même si vous n'en avec pas réellement besoin) :
f(x)=;)*sin(x)

En bref, trouvez de telle manière qu'on n'obtienne qu'une seule "vague" complète de la fonction sin(x)

Bon casse-tête !

peut-être bien

[upium666]

peut-être bien

J'en avais trouvée une autre mais c'est ça
Bravo :zen: !

[manoa]

J'en avais trouvée une autre mais c'est ça
Bravo :zen: !

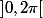
sauf qu'elle est définie sur comme remarqué d'ailleurs par Skullkid (05/06/2012 21h 17).

[newman]

dans ce cas là il suffit de prolonger par continuité en posant f(0)=f(2*Pi)=0..

Sinon je vous avoue ne pas avoir bien saisi l'essence même de l'exercice...c'est farfelu je trouve^^

[Judoboy]

J'en avais trouvée une autre mais c'est ça
Bravo :zen: !

T'as quand même eu droit y a 2 semaines à un post super détaillé qui répond à la question et qui t'explique pourquoi la question est idiote, ça te ferait vraiment mal de le lire ?

Pour le retrouver c'est simple, c'est le post que t'as pas lu parce qu'il était trop long et qu'il avait l'air trop compliqué.