Deux fonctions périodiques

par **Imod** » 14 Oct 2008, 10:11

Un problème que j'ai vu sur le forum il y a quelques jours et qui s'est apparemment volatilisé :doh:

Existe-il deux fonctions périodiques f et g de R dans R telles que f+g soit égale à l'identité ?

Il me semble qu'il y a une infinité de solution , qu'en pensez-vous ?

Imod

par **le_fabien** » 14 Oct 2008, 11:36

Bonjour Imod,
Ouais je pense aussi . Si f(x)=sin²x et g(x)=cos²x , là au moins il y a une solution.
Mais en ce qui concerne l'infinité de solution, je ne sais pas démontrer.

par **Doraki** » 14 Oct 2008, 11:45

cos²(x) + sin²(x) ça fait pas x mais 1.
De toutes façons tu peux pas montrer l'existence de ces fonctions sans utiliser l'axiome du choix donc toutes les formules que tu peux imaginer vont rater.

par **le_fabien** » 14 Oct 2008, 11:47

Doraki a écrit:cos²(x) + sin²(x) ça fait pas x mais 1.
De toutes façons tu peux pas montrer l'existence de ces fonctions sans utiliser l'axiome du choix donc toutes les formules que tu peux imaginer vont rater.

AHHHh La fonction identité! Je pensais à l'unité :doh:
Donc mon post est à oublier.

par **mathieuH** » 14 Oct 2008, 12:01

je remet ce que j'avais posté avant que ca disparaisse...

une fonction

périodique est bornée donc la somme de deux fonctions périodiques est forcément bornée (au contraire de l'identité).

Si elle ne sont pas définies sur

, c'est peut etre faisable, mais j'ai des gros doutes...

On peut déjà montrer qu'il est nécessaire d'avoir des périodes non commensurables (

).

par **Patastronch** » 14 Oct 2008, 14:05

Ben il peut y avoir des fonctions periodique non bornées si elles sont pas continues non ?
La fonction tan(x) par exemple.

par **mathieuH** » 14 Oct 2008, 15:10

tan n'est pas définie sur

.

Mais en fait on peut la prolonger pour qu'elle le soit.
Donc, ce que je disais avant est faux. Une fonction périodique n'est pas forcément bornée.

Ca remet tout à la case départ.

La seule chose vraie est que leurs périodes sont incommensurables.

par **Dominique Lefebvre** » 14 Oct 2008, 15:13

mathieuH a écrit:je remet ce que j'avais posté avant que ca disparaisse...

une fonction périodique est bornée donc la somme de deux fonctions périodiques est forcément bornée (au contraire de l'identité).

Si elle ne sont pas définies sur , c'est peut etre faisable, mais j'ai des gros doutes...

On peut déjà montrer qu'il est nécessaire d'avoir des périodes non commensurables ().

Bonjour,
Toute discussion non conforme au réglement du forum est modérée. Si tu t'aperçois qu'une discussion a disparue c'est qu'elle été non conforme. C'est aussi simple que cela....

par **Patastronch** » 14 Oct 2008, 16:06

mathieuH a écrit:La seule chose vraie est que leurs périodes sont incommensurables.

Oui ca c'est évident, sinon la fonction resultante serait périodique si je ne m'abuse, et la fonction identité est loin d'être périodique

par **ThSQ** » 14 Oct 2008, 18:17

Imod a écrit:Il me semble qu'il y a une infinité de solution , qu'en pensez-vous ?

Je pense bien ! On peut en construire "autant" que de fonctions réelles.

par **Imod** » 14 Oct 2008, 18:28

ThSQ a écrit:Je pense bien ! On peut en construire "autant" que de fonctions réelles.

Rain' a écrit:Il me semble que s'il y en a une alors il y en a une bonne infinité en effet :id:

Ouah , les jeunes , toujours à chambrer les anciens !!!

Pourquoi en existe-t-il une ? ( il y a bien de l'axiome du choix la dessous :doh:)

Imod

par **miikou** » 14 Oct 2008, 18:31

en effet si il y en a une, on en deduit une infinité.
serait-ce possible d'exhiber un couple solution ?

par **Imod** » 14 Oct 2008, 18:35

miikou a écrit:en effet si il y en a une, on en deduit une infinité.
serait-ce possible d'exhiber un couple solution ?

Enfin du soutien :zen:

Ne cherche pas trop parmi les fonctions usuelles mais plutôt en utilisant une base de

considéré comme un

-espace vectoriel :we:

Imod

par **miikou** » 15 Oct 2008, 19:57

je vois pas imod, tu peux me dire comment tu demontres l'existence ?

par **Doraki** » 15 Oct 2008, 22:53

Soit

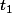et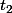

les périodes de f et g.

Soit G le sousgroupe de

engendré par

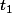et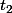

.
On regarde le groupe quotient

.
Soit

une fonction de choix qui à chaque classe

associe un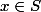

(il faut l'axiome du choix)

G est isomorphe à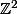

(sinon f+g serait périodique et l'identité n'est pas périodique)
Donc

est en bijection avec

via

On regarde maintenant f et g comme fonctions de

dans

:

Soit

.
on a

Comme g ne dépend pas de q,

, et donc comme f ne dépend pas de p,
on a

.
De même,

.

On en déduit que f et g sont de la forme :

où

est une fonction absolument quelconque.

Réciproquement, toutes les paires de fonctions (f,g) de cette forme sont des solutions au problème.

par **Imod** » 16 Oct 2008, 10:59

Mon approche était moins formelle ( 20 ans de collège ça endort :dodo: ) . L'existence d'une base de Hammel ( base de R considéré comme un Q-espace vectoriel ) permet de prouver l'existence de telles fonctions .

Imod

Deux fonctions périodiques

Deux fonctions périodiques

Qui est en ligne